TALBLINDHED –EN FORSKNINGSOVERSIGTAfdelingsleder: Kræn Blume JensenAfdelingen for socialpolitik og velfærdsydelserUndersøgelsens følgegruppe:Bent Lindhardt, RUCPernille Pind, Pind og BjerreLena Lindenskov, DPUMichael Wahl Andersen, PAPSISSN: 1396-1810ISBN: 978-87-7119-205-6e-ISBN: 978-87-7119- 206-3Layout: Hedda BankForsidefoto: Hedda BankOplag: 300Tryk: Rosendahls – Schultz Grafisk A/S� 2013 SFI – Det Nationale Forskningscenter for VelfærdSFI – Det Nationale Forskningscenter for VelfærdHerluf Trolles Gade 111052 København KTlf. 33 48 08 00[email protected]www.sfi.dkSFI’s publikationer kan frit citeres med tydelig angivelse af kilden.

FORORDDenne forskningsoversigt er udarbejdet på bestilling af Ministeriet forBørn og Undervisning. Oversigten skal belyse begrebet dyskalkuli ellertalblindhed, test for skolebørn i forskellig alder samt former for støtte tilde elever, det drejer sig om. Målgruppe for forskningsoversigten er pri-mært matematiklærere og andre, der på forskellig vis beskæftiger sig medundervisning i matematik. Sekundært er målgruppen skoleverdenen i al-mindelighed.Studenterne Maj Bjerre og Maja Thorsteinsson har indsamlet ogrefereret litteratur, videnskabelig assistent Lena Bech Larsen har stået forbearbejdelsen af det og skrevet kapitlerne 2-7, mens seniorforsker SteenBengtsson har ledet projektet og skrevet kapitel 1.Vi har under arbejdet fået værdifulde kommentarer fra BentLindhardt, Pernille Pind, Lena Lindenskov, Michael Wahl Andersen, Pe-ter Weng, Lene Østergaard Johansen, Steen Polk, Henrik Skovhus ogKarin Jessen såvel mundtligt på møder, mens vi arbejdede på opgaven,som skriftligt i de senere faser. Vi takker for dette værdifulde input, udendet havde arbejdet slet ikke været muligt.København, november 2013AGI CSONKA

RESUMÉDenne rapport giver en oversigt over området talblindhed (dyskalkuli),særligt i Danmark, Norge, Sverige og Storbritannien. Undervisningsmini-steriet vil sætte en udvikling af test for dyskalkuli (talblindhed) i gang forskolebørn samt udarbejde elektroniske vejledninger med eksempler på oghandlemuligheder for, hvordan relevant vidensbaseret undervisning kanblive struktureret i almenundervisningen for elever med dyskalkuli gen-nem hele skoleforløbet. I den forbindelse er formålet med denne over-sigt at skabe et overblik over dyskalkuli-feltet, hvad det indebærer, hvilkekriterier der gør sig gældende, hvilke testmetoder der bliver anvendt, oghvor tidligt en indsats kan igangsættes.BAGGRUND

Der er efterhånden åbnet op for erkendelsen af, at nogle mennesker hardet særligt svært med tal. Mennesker, der er svært udfordret i forhold tilat håndtere tal, kan være svært begrænset i deres uddannelses- og ar-bejdsliv og ikke mindst i forhold til almindelige dagligdagsaktiviteter. Iskolen kan det fx omhandle basale regneopgaver (plus, minus, gange ogdividere) samt at aflæse en tabel eller en graf. I dagligdagen kan det fxdreje sig om at håndtere telefonnumre, læse en bus- eller togplan og hol-de styr på tiden eller privatøkonomien.

Fænomenet dyskalkuli er en anerkendt tilstand og diagnose medbetegnelsen ”81.2 Specifik regnevanskelighed (dyskalkuli)”1i WHO’sICD-10 (International Classification of Diseases and Related HealthProblems). ICD-10 er et katalog over alle officielle diagnoser2. Kort sagter der tale om personer, der har ”… tilbagestående regnefærdigheder,som ikke skyldes mental retardering eller mangelfuld skolegang. Regne-vanskeligheder omfatter manglende evne til at beherske basale regnefær-digheder…”.Mange kender slet ikke til diagnosen dyskalkuli, selvom fæno-menet efterhånden er anerkendt blandt praktikere og forskere. Lærere ogskoler kan opleve, at enkelte elever har svært ved at beherske basale reg-nefærdigheder på trods af interesse og evner. Det er svært for lærere ogskoler at identificere og hjælpe de elever, der eventuelt har dyskalkuliuden viden om dyskalkuli og indsigt i, hvad det indebærer. De konkretekriterier for dyskalkuli er imidlertid ikke yderligere specificeret i ICD-10,og definitionen er derfor relativ åben for fortolkning. Blandt både prak-tikere og forskere findes der derfor også mange forskellige tilgange, somsamtidig beskriver forskellige variationer af fænomenet.RESULTATER

Der findes generelt ikke meget forskning om dyskalkuli. Internationaltset findes der mange videnskabelige og øvrige typer af informationer omtalblindhed, dog stritter de i mange forskellige retninger både som helhedog hver især. Videnskabeligt set er der dermed mange uklarheder om-kring fænomenet. I Danmark findes der stort set ingen reel forskning omemnet, og samtidig er de undersøgelser, der findes i Danmark, centreretomkring få videnspersoner. I de senere år har der været stigende inter-esse for og et øget fokus på elever med matematikvanskeligheder, hvilketogså er smittet af på interessen for dyskalkuli. Imidlertid arbejder bådeforskere og praktikere ofte ud fra forskellige begreber, definitioner ogkriterier, som ikke nødvendigvis er veldokumenterede. Ligeledes variererestimatet af, hvor mange personer der har dyskalkuli, afhængigt af hvor-dan dyskalkuli bliver defineret. Eksperter vurderer, at mellem 1-6 pct. afbefolkningen har dyskalkuli.Generelt mangler der altså forskningsmæssig viden om dyskalku-li. Der mangler endvidere konsensus om, hvilke kriterier der gør sig gæl-1. Eller ”Disordo aritmetici specificatus (dyscalculia)”.2. Danmark er medlem af WHO, hvormed diagnosen officielt er anerkendt her i landet.

dende i forhold til bestemmelsen eller diagnosticeringen af dyskalkuli,hvordan disse kriterier skal undersøges, samt hvordan støtten efterføl-gende skal tilrettelægges.I litteraturen findes mange og meget forskellige holdninger tilfeltet, dets termer, definitioner, test og støtteformer. En grundlæggendeudfordring er netop den manglende konsensus, hvilket begreb der skalanvendes, og hvad begrebet skal dække over. Litteraturen har variation ibegrebsvalg, definition og graden af afgrænsning. Denne variation ermed til at skabe forvirring omkring fænomenet.Denne oversigt bidrager med et overblik over, hvordan dyskal-kuli kan defineres, hvilke testmaterialer der allerede anvendes, hvilkestøtteformer der sættes ind med, og om der er forskning, der understøt-ter, at anvendte støtteformer har en virkning i forhold til dyskalkuli. Meddenne oversigt er det vores hensigt at skabe et overblik, der kan dannebaggrund for det videre forløb med at udvikle en anvendelig test til be-stemmelse af dyskalkuli.DATAGRUNDLAG

Empirien bygger i første omgang på en klassisk litteratursøgning på om-rådet. Da det drejer sig om et meget lidt udforsket område, kan dennemetode imidlertid ikke spille den hovedrolle, den ville indtage på mangeandre felter. Det meste materiale har vi derfor fremskaffet gennem enidentifikation af eksperter i Danmark, Sverige, Norge og Storbritannien.De udvalgte lande er lande, som er relevante at sammenligne Danmarkmed. På opfordring fra danske eksperter inddrager vi dog også enkeltevidenskabelige forfattere og undersøgelser fra andre lande end de nævnte.I forhold til sidstnævnte vil vi begrænse os til de mest fremtrædende afhensyn til den tidsmæssige begrænsning.

HOVEDRESULTATERHvor sikker er den viden, vi har om dyskalkuli, hvor sikre er de test, derfindes til at teste mindre og større børn for dyskalkuli, hvor sikker videnhar vi om forholdet mellem de forskellige former for matematikvanske-ligheder og baggrunden for dem, og hvor sikker viden har vi om effektenaf de støtteformer, der findes i forhold til dyskalkuli og matematikvan-skeligheder i almindelighed?Vi ved en del, men der er også meget, vi ikke ved, og vores vi-den om det vi ved, er ikke alt for sikker, lige som forskere på områdetgiver forskellige svar på mange af spørgsmålene.

Der er grund til at tro på, at dyskalkuli findes. Der er nogle elementæreevner til talforståelse og opfattelse af mængder, som kan ses hos spæd-børn allerede en uge efter fødslen. Dette peger i retning af, at dyskalkuli,forstået som evnen til at abstrahere antal, er medfødt. Det vil sige, at derfindes en intuitiv talfornemmelse, som kan mangle hos enkelte menne-sker, og som kan gøre det specielt vanskeligt for disse mennesker at for-stå selv simple forhold, der har med tal og mængder at gøre. Det styrkertroen på fænomenet dyskalkuli ganske meget, at neurologerne kan udpe-

ge et område i hjernen, som beskæftiger sig med forståelsen af tal ogmængder.Neurologisk forskning opstiller og behandler forskellige hypote-ser, og videnskabelige artikler slutter ofte med en pointering af områdetsjomfruelighed og dets behov for mere forskning. Forskningen kan medandre ord ikke sige, hvad der gør det omtalte område af hjernen i standtil at bearbejde tal og mængder, eller hvordan denne evne udvikler sigover tid. De ved heller ikke, hvad der bevirker, at den undertiden mang-ler. Da der er en arvelig faktor i dyskalkuli, kan det betyde, at der på sigter mulighed for, at forskningen vil kunne finde frem til et eller flere ge-ner, som har en betydning i forhold til dyskalkuli. På den anden side ty-der forskningen på, at arvemassen alene ikke er afgørende fx i tilfælde,hvor kun den ene af to enæggede tvillinger har dyskalkuli.Der findes mange forskellige tilgange til feltet, hvor forskere ogpraktikere anvender forskellige begreber om det samme fænomen, ellerbruger de samme begreber om forskellige relaterede fænomener. Tildenne rapport anvender vi betegnelsen ”dyskalkuli” eller ”talblindhed”,som vi bruger synonymt om en mangel på medfødte evner til at håndteretal og mængder. Matematikvanskeligheder kan være andet end dyskalkuli.Begrebet matematikvanskeligheder forstår vi som et meget bredere be-greb, som vi benytter om det forhold, at elever kan have vanskelighederknyttet til faget matematik og med baggrund i mange årsager, såsom ge-nerelle vanskeligheder, langsom udvikling af faglige færdigheder, mate-matikangst, trivselsproblemer mv.Vi er nået frem til ovenstående begrebsvalg og skelnen mellembegreber ved at se på en lang række definitioner og undersøgelser foreta-get af både forskere og praktikere på feltet. Hvordan vi er nået frem tilvores begrebsvalg og -skelnen beskrives nærmere i rapporten. Selvommange her i landet slet ikke kender begrebet talblindhed eller dyskalkuli,mener vi, det er velegnet til at beskrive erfaringer, matematiklærere harmed enkelte elever.Det drejer sig om elever, der har svært ved at beherske basaleregnefærdigheder på trods af interesse og evner, hvor læreren opleverhelt at mangle mulighed for at afhjælpe disse vanskeligheder. Det ersvært for lærere og skoler at identificere og yde et relevant undervisnings-tilbud uden viden om dyskalkuli og indsigt i, hvad det indebærer. Detteaktualiserer behovet for undersøgelser, herunder nærværende status.

I forbindelse med definitionen af dyskalkuli refererer vi en om-fattende debat, der har fundet og stadig finder sted i de skandinaviskelande. Den handler om, hvorvidt dyskalkuli findes eller ej, om det gavnereleven, at vi identificerer dyskalkuli, om dette har en uheldig virkning iform af stempling, og hvorvidt en identifikation af dyskalkuli betydernoget for den pædagogik, der skal til. Debatten kæder ofte disse emnersammen med spørgsmålet, om problemer med matematik skal klares forden enkelte elev eller i klassen. Lidt forsimplet samler debatten sig omspørgsmålet: hvorvidt vi skal tale om dyskalkuli, eller hvorvidt vi skal taleom matematikvanskeligheder i bredere forstand. Om det handler omnogle meget specifikke evner, eller om det handler om forholdet til fagetmatematik generelt. Dertil er det også et spørgsmål om, hvordan diagno-ser er relevante i en tid med omlægning til øget inklusion.Næsten alle forskere og praktikere har en holdning til dettespørgsmål, og nogle har en stærk aversion imod begrebet ”dyskalkuli”.Denne stærke modstand mod begrebet har især været fremherskende ien årrække omkring århundredeskiftet. På baggrund af denne oversigtover forskningen i dyskalkuli og til dels matematikvanskeligheder, som viher fremlægger, har vi imidlertid konkluderet, at begge begreber har enberettigelse. Der findes meget specifikke regnevanskeligheder, som gørdet vanskeligt for nogle få procent af eleverne i skolen at lære at regne oghave at gøre med tal, og der findes mange andre former for matematik-vanskeligheder, som kan have forskellig baggrund.Den norske forsker Olof Magne – som er ”grand old man” iskandinavisk dyskalkuliforskning – har først i sin karriere talt om dyskal-kuli og er senere gået over til at bruge ordet ”dysmatematik”. Dernæstfandt han, at disse ord i for høj grad placerede problemet hos eleven, oggik over til at tale om SUM-elever (specielle undervisningsbehov i mate-matik). Denne betegnelse skal understrege, at der er tale om et samspilmellem elev og omgivelser. Det ser samtidig ud til, at Magne gennemårene har bevæget sig fra en interesse i meget specifikke vanskelighedertil en interesse for mere generelle matematikvanskeligheder.Brian Butterworth – en britisk dyskalkuliforsker, der er en af demest indflydelsesrige på området i dag – mener, at begge begreber er re-levante, men at der er tale om to forskellige ting. Der er ingen grund til atslå de to fænomener i hovedet med hinanden. Fordelen ved at have etdyskalkulibegreb, som handler om helt specifikke medfødte ”instinkter”,er, at man kan søge efter en erstatning eller kompensation for dem, og

det er måske noget andet end at løse problemerne for elever med meregenerelle matematikvanskeligheder.Vi ser på forskellige definitioner af dyskalkuli. Begrebet bliverdefineret i diagnosesystemerne ICD-10, som bliver benyttet i Danmarkog flere andre europæiske lande og DSM-4, som indtil for nylig blev be-nyttet i USA. Her er man for nylig gået over til DSM-5, som ikke længerearbejder med dyskalkuli som en selvstændig diagnose, men slår det sam-men med blandt andet dysleksi til et bredere begreb, specifikke lærings-vanskeligheder. Der er imidlertid ikke, som nogle har forstået det, taleom, at dyskalkuli er gledet ud af det amerikanske diagnosesystem.Vi ser endvidere på en række faglige perspektiver på problema-tikken. Det neurologiske perspektiv, som har fået stadig større betydninggennem de senere år, er det perspektiv, der rummer de bedste begrundel-ser for at tale om de specifikke vanskeligheder, der dækkes af ordet dy-skalkuli. Det neurologiske perspektivs stigende indflydelse er vel ogsåbaggrunden for, at begrebet ”dyskalkuli” er kommet tilbage efter at haveværet trængt i baggrunden på grund af den indflydelse, andre perspekti-ver havde. Vi tænker på det sociologiske, det psykologiske og især detdidaktiske perspektiv, som vi også kommer ind på.Endelig kommer vi ind på forskellige typer af dyskalkuli. Des-værre er der ikke én bestemt logisk måde at dele disse op på, men for-skerne kommer med flere typologier, der alle virker nogenlunde lige ri-melige og nærmere beset viser sig at handle om meget af det samme. Énmåde er at dele op i 1) problemer med at tælle, regne og anvende regler,2) problemer med hukommelse og sprog og 3) problemer med form,mønstre, forhold og rum. Disse tre typer problemer kan så kaldes hen-holdsvis procedurale, semantiske og visuo-spatiale. Flere bemærker, atdyskalkuli ikke nødvendigvis betyder, at eleven har vanskeligt ved at læreabstrakt matematik på gymnasieniveau.Som nævnt kan matematikvanskeligheder have mange årsager.Hvis der er tale om konsekvenser af kognitive eller emotionelle proble-mer, falder de imidlertid ikke ind under definitionen på dyskalkuli, selvom dyskalkuli kan føre til sekundære vanskeligheder som angst og dårligtselvværd. Dyskalkuli handler specifikt om nogle elementære færdigheder.Dyskalkuli kan godt forenes med gode eller middel præstationer i mereavanceret, abstrakte matematik. Derimod indebærer dyskalkuli typiskvanskeligheder med ting som at aflæse et analogt ur, finde et husnummer

eller forstå en togplan. På baggrund af vores litteraturgennemgang er vinået frem til følgende forslag til en brugbar definition:Dyskalkuli er en funktionsnedsættelse, der kan have negativ ind-virkning på den berørtes uddannelses- og arbejdsliv. Tilstandendrejer sig om tilbagestående regnefærdigheder, som ikke mod-svares af tilsvarende tilbagestående færdigheder på andre felter.De specifikke regnevanskeligheder omfatter påfaldende vanske-ligheder med at forstå og håndtere basal talbehandling, såsom atsammenligne tal og antal i mængder eller tælle små antal gen-stande. I forlængelse heraf er der påfaldende vanskeligheder vedaddition, subtraktion, multiplikation og division. Tilstanden om-fatter ikke nødvendigvis vanskeligheder med mere abstrakte ma-tematiske færdigheder i algebra, trigonometri, geometri og kom-plekse beregninger. Vi taler ikke om dyskalkuli, hvis baggrundenfor vanskelighederne er mental retardering eller mangelfuld sko-legang. Dog kan tilstanden omfatte kognitive problemer sommangelfuld semantisk hukommelse og arbejdshukommelse.TEST

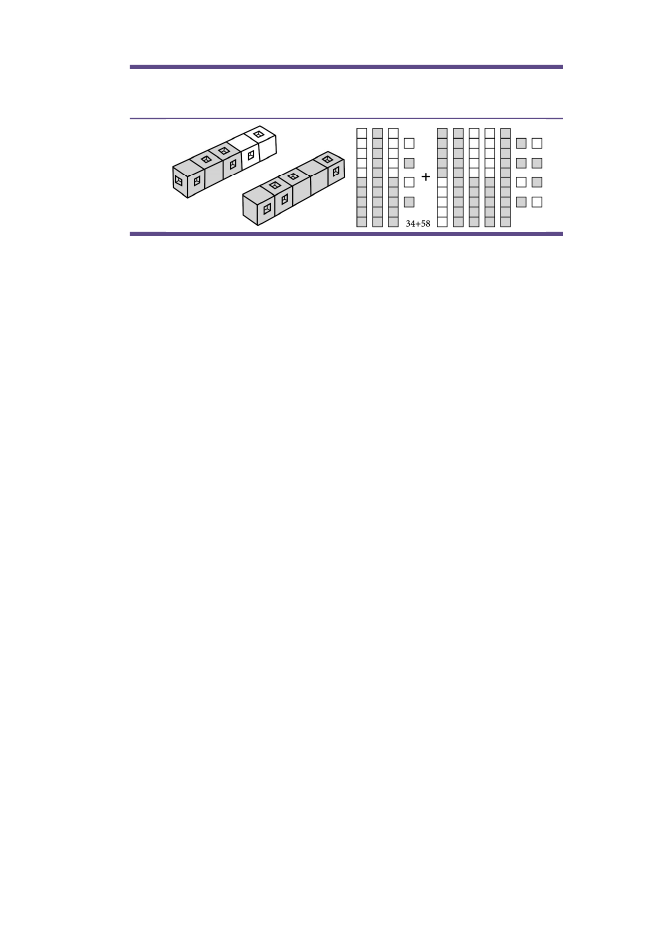
Nogle test bygger alene på tal – i nogle tilfælde i form af et tilfældigt antalprikker, så man undgår talsymbolet. På den måde kommer et tal til atblive repræsenteret af en mængde. Men mange test indeholder mere endde helt simple tal og mængdeøvelser. Ofte viser de cifre. Det vil fx værenødvendigt, hvis en test skal vise, om eleven forstår positioner i ti-talsystemet. Dermed inddrager de noget mere end de rene tal og mæng-der, og hjernen vil inddrage flere områder beliggende helt andre steder tilat løse de opgaver.Test vil således i mange tilfælde belyse noget mere end den ”rene”dyskalkuli. En validering af test kan ske ved at undersøge, i hvilket om-fang forskellige test vil udpege de samme elever som dem, der har dy-skalkuli. En sådan validering er vi dog ikke stødt på.Det har også været et formål med denne forskningsoversigt atfinde testmaterialer, som vi derfor også præsenterer i denne tekst. Vi skaldog understrege, at det i langt de fleste tilfælde ikke har ligget inden forvores rammer at fremskaffe disse testmaterialer og undersøge dem nær-mere, så vi er her kun i stand til at give en andenhåndsberetning. Somindledning til denne ser vi på argumenterne for og imod brugen af test,samt hvordan der testes.

Argumenterne mod testning hænger til dels sammen med denmodstand mod begrebet dyskalkuli, vi allerede har omtalt. Disse argu-menter går på, at testning er et uheldigt element i en undervisning, fordidet sætter stempel på eleverne, og fordi det samler opmærksomhedenom fejl og problemer med den kendte psykologiske virkning, at det bli-ver vanskeligere at slippe af med dem. Der er næppe tvivl om, at kritikofte er meget upædagogisk, og at læreren skal gøre meget for at modvir-ke denne effekt. En anden indvending mod test er, at de fører til ”test-læring” – altså at læreren lægger vægt på de områder, som denne vedindgår i test, men springer let hen over de ting, der ikke bliver testet.Omvendt er der også fordele ved at benytte test. For eksempelkan test give opmærksomhed på mangfoldighed i elevgrundlaget og be-hovet for undervisningsdifferentiering samt bidrage med et fokus i plan-lægningen af undervisningen. En fordel er også, at det er en metode til atfå eleverne til at repetere et stofområde. Dette gør sig dog ikke gældendeved en dyskalkulitest, som netop ikke tester i stof, som eleverne har lært,men i evner de besidder forud for, at de lærer noget. For dyskalkulitestener den fordel, at den giver mulighed for at pege på de elever, der har brugfor en meget speciel indsats i god tid for at have en chance for at følgemed i matematikken. Vi vil understrege det synspunkt, at en dyskal-kulitest kun har mening, hvis den kan pege på denne gruppe elever, oghvis der så findes en indsats, der vil gøre det muligt for dem at kompen-sere for de manglende elementære evner.Vi ser på en række test for dyskalkuli:Butterworths Dyscalculia Screenerbestår af forskellige opgaver, fxmed at se hvor mange prikker der er i en ramme, der indeholder ganskefå samt se, hvor der er flest prikker i to rammer. Testen er computerba-seret og registrerer både, om eleven giver rigtigt eller forkert svar, oghvor lang tid det tager eleven at svare – det sidste for at det skal vise no-get om, hvilke strategier eleven har brugt til at løse opgaven: Hvis eleventæller for at løse en simpel opgave, som de fleste umiddelbart kan se løs-ningen på, kan det være tegn på dyskalkuli. Screeneren er dog blevet kri-tiseret, da en længere bearbejdningstid til at løse en opgave også kan væretegn på, at eleven er nervøs eller keder sig. Butterworths DyscalculiaScreener er beregnet til elever på 6-14 år.Emerson & Babties Dyscalculia Assessmentgår videre ad samme spor.I ordet ”assessment” (til forskel fra screener) ligger, at det drejer sig omen mere grundig test eller vurdering. Den består først af en samtale med

eleven, og derpå er der en test, hvor eleven ikke blot løser opgaverne,men samtidig fortæller om sin strategi for at løse dem. Endelig omfatterden også information fra forældre, lærere og andre professionelle. Dennetest viser ikke blot, om der er tale om specifikke vanskeligheder med ma-tematikken, men siger også noget nærmere om, hvilke typer af specifikkevanskeligheder eleven har.McCarthy-Hesse-Gilhams Basic Number Screening Tester en screening,der kan benyttes på en hel klasse ad gangen. Opgaverne bliver givetmundtligt, således at eventuelle læsevanskeligheder ikke får betydning forelevernes mulighed for at løse opgaverne. Det har fx betydning i forbin-delse med at kunne adskille dyskalkuli fra dysleksi. De to funktionsned-sættelser kan forekomme sammen, og gør det i mange tilfælde, men dehar i mindst lige så mange tilfælde intet med hinanden at gøre.Endelig ser vi påChinns Dealing with Dyscalculia,som omfatter entest af præstationsniveau, et spørgeskema om angst i forbindelse medmatematik, en test for viden om basale fakta samt noget om elevenstænkning og strategier ved løsning af opgaver. Som det fremgår af be-skrivelsen, er der her tale om en test, som ikke bare dækker dyskalkuli,men også går ind på viden og følelser. Den ligger således i et grænseom-råde, hvor ikke kun de specifikke vanskeligheder med tal og mængder,men også de bredere matematikvanskeligheder er kommet med ind i fo-kus.Forskningsoversigten nævner endvidere et antal test, der ikkespecielt angår dyskalkuli, men nærmere handler om matematikvanske-ligheder i bredere forstand.STØTTEFORMER

I forhold til støtteformer er vi heller ikke stødt på evalueringer af støtte-former, som lever op til evidenskrav på trin A eller B3. Forudsat at derforegår en testning af elever, som kan identificere elever med dyskalkuli,vil det være en relativ enkel sag at foretage en evaluering af disse test ogdertilhørende støtteformer på højt evidensniveau4.Da der ikke har været sat systematisk ind i forhold til dyskalkuli ide skandinaviske lande, hvor man mere har interesseret sig for generelle3. Socialstyrelsens vidensdeklaration side 16.4. Hvis støtten sættes ind over for den enkelte elev, kan eleverne fordeles på støtteformer ved lod-trækning. Hvis støtten sættes ind over for en klasse, kan klasserne fordeles på støtteformer vedlodtrækning. I begge tilfælde vil det være muligt at leve op til kravene til et RCT-forsøg, (Rando-mized Controlled Trial).

matematikvanskeligheder, er der heller ikke udviklet egentlige støttepro-grammer. Der er dog en del støtteformer og materialer, som vi skalkomme tilbage til.Først vil vi imidlertid nævne, at der hidtil har været mest op-mærksomhed på, hvordan den almindelige evne til matematisk tænkningkan udvikles hos børn, også i førskolealderen. Det er også muligt at testebørn før skolealderen – der findes således et screeningsværktøj MIOmed dette formål. En tidlig indsats for at styrke den matematiske tænk-ning kan altså sættes ind allerede fra to-års-alderen.En sådan indsats inddrager typisk flere sanser i forbindelse medord, billeder, fysisk aktivitet, hverdagssituationer og lege. Der findes for-skellige materialer, som kan anvendes af forældre og børneinstitutioner.Det drejer sig ikke om matematik med symboler som i skolen, men omlogisk tænkning og forståelse af tal og forhold i hverdagssituationer, sombørn udvikler, længe før de er i stand til at omsætte det til symbolsprog.Olof Magne har således en legedidaktik, som han betegner-”livsmatematik”. Den handler om det, han betegner P-området medbegreber som alle, mange, ingen, nogle og få samt om T-området, somdækker over forståelse af tal og mængder samt G-området, som drejersig om geometri, rum, balance og kropskontrol og endelig ASMD-området, som omfatter de elementære regnearter addition, subtraktion,multiplikation og division.Når det drejer sig om de specifikke vanskeligheder med matema-tik, som betegnes dyskalkuli, kan det være vanskeligt at styrke og udviklenogle evner, som eleverne ikke har. I den forbindelse skal man måskemere tænke på at kompensere og give eleverne hjælpemidler, som de kanbenytte til at erstatte de evner, de fleste andre elever har. Et almindeligthjælpemiddel er de såkaldte Cuisenaire-stænger5, som er stænger bestå-ende af et antal terninger, som illustrerer tal mellem et og ti. De kan bådebruges til at illustrere små tal og til at vise noget om positioner i titalssy-stemet.Elever med dyskalkuli kan også hjælpes med flittig brug af enalmindelig lommeregner, ligesom der findes nogle spil, som kan hjælpedem. Der findes også specielle lommeregnere: Multimedia Interactive5. Cuisenaire-stænger eller centicubes er et læringsværktøj, der består af små firkantede klodser iforskellige farver, som kan klikkes sammen og skilles ad igen (lidt som legoklodser). Formen erdirekte knyttet til læringsindholdet, da centicubes-værdier alle kommer til udtryk gennem klod-sernes fysiske form. Derudover har klodsen ingen overflødig funktion, som kan vildlede bruge-ren.

Forskningsoversigten har vi søgt at bygge op på en måde, så den kan an-vendes som et opslagsværk.Kapitel 2 beskriver hvordan denne oversigt er tilrettelagt oggennemført. I dette kapitel beskriver vi først litteratursøgningsprocessen,og dernæst introducerer vi kort forskningsområdet dyskalkuli set i et hi-storisk perspektiv.Kapitel 3 består af en kortlægning af definitioner af dyskalkuliprimært i Sverige, Norge og Storbritannien. Kapitlet uddyber blandt an-det, hvilke definitioner der bliver anvendt, hvorvidt definitionerne opere-rer med flere typer af dyskalkuli, og hvordan disse typer nærmere er ka-rakteriseret, herunder hvilke forudsætninger eller færdigheder der er på-virket. Hensigten med dette kapitel er at vurdere, hvad der hersker en viskonsensus om og på det grundlag byde ind med et forslag til en konkretdefinition, vi kan anvende i det videre forløb.Kapitel 4 er en kortlægning af eksisterende testmateriale. Her be-skriver vi eksisterende testmateriale og ser på, hvordan det bliver an-vendt, hvilke målgrupper der er tale om, hvornår test kan anvendes, oghvilke færdigheder de forskellige test afdækker. Hensigten er også her atfå en vurdering af, om der hersker en vis grad af konsensus omkring,hvad det er relevant at teste i forhold til dyskalkuli, samt hvordan det kanforegå.Kapitel 5 er en afdækning af støtteformer, der kommer i anven-delse som konsekvens af testresultater samt støtteformer, der i øvrigt ernævnt i litteraturen. Denne del af kortlægningen søger at klargøre, hvilkeformer for støtte der rent faktisk sættes ind med og på hvilke tidspunktersom konsekvens af fundne testresultater. Dertil er hensigten at belyse,om der er forskning, der støtter, at de anvendte støtteformer rent faktiskhar en inkluderende og udviklende virkning i forhold til elever med dy-skalkuli, og som kan være til gavn for hele klassen.

De sidste to kapitler, kapitel 6 og 7, giver henholdsvis et overblikover eksperter og netværk i Danmark, Sverige, Norge og Storbritanniensamt enkelte eksperter uden for de nævnte områder, hvor vi lægger vægtpå de mest fremtrædende på feltet. Sidstnævnte eksperter har vi fået an-befalet af de danske eksperter, vi løbende har haft kontakt til.Den samlede kortlægning har primært fokus på nyere forskningpå området og inddrager samtidig aktuelle problemstillinger. Der kanderfor forekomme gentagelser, da den samme forskning anvendes medforskellige fokusområder i de forskellige kapitler for at belyse de forskel-lige aspekter. Det betyder imidlertid også, at de enkelte kapitler kan læsesuafhængigt af hinanden. Kapitlerne henviser til hinanden på de steder,hvor vi har fundet, at det giver mening.Sidst i rapporten er der en ordforklaring baseret på litteraturen.Derudover har vi udarbejdet en skematisk oversigt, som er at finde sidst irapporten (bilag 1).

Formålet med denne oversigt er at skabe et overblik over feltet og samti-dig finde frem til områder, hvor der er konsensus omkring definitioner afdyskalkuli og metoder til måling af dyskalkuli. En endelig afgrænsning afdyskalkuli vil derfor være en del af konklusionen (jf. kapitel 3).Som udgangspunkt anvender vi WHO’s ICD-10 til at definereDyskalkuli (specifikke regnevanskeligheder). WHO’s definition er imid-lertid ikke tilstrækkeligt detaljeret i forhold til, hvilke specifikke regne-vanskeligheder det drejer sig om, og hvilke konkrete kriterier der indgår.Det efterlader det konkrete indhold af specifikke vanskeligheder relativtåben for fortolkning.Den nuværende definition betyder, at den forskning, der beskæf-tiger sig med regnevanskeligheder i bred forstand, kan karakteriseres somdyskalkuli-forskning. Dyskalkuli-forskningen spænder over mange for-

skellige fagdiscipliner og emner, blandt andet neurologi, psykologi, socio-logi, didaktik osv. Den faglige spændevidde i dyskalkuli-forskningen præ-ger forskellige opfattelser af dyskalkuli og tolkninger af definitionen,hvor både praktikere og forskere opererer med forskellige opfattelser af,hvad dyskalkuli er. For det første kan dette tyde på, at WHO’s definitionikke bliver anvendt. For det andet kan dette tyde på, at hvis den bliveranvendt, så tolkes den meget forskelligt.Flere danske eksperter påpeger, at WHO’s definition formentliger under forandring, idet ICD-klassifikationen har en tendens til at læggesig op ad den amerikanske klassifikation DSM (Diagnostic and StatisticalManual of mental Disorders) fra APA (American Psychiatric Associati-on).6APA har helt afskaffet specifikke vanskeligheder i det amerikanskemodstykke. I den nyeste (maj 2013) og femte version af den amerikanskeklassifikation, DSM-5, bliver der lagt op til en anderledes tilgang end tid-ligere i forhold til læringsvanskeligheder. I denne femte version udvideskategorien ”læringsvanskeligheder” for at øge den diagnostiske præcision,og for at den mere effektivt skal være målrettet praksis. I denne femteversion er ”specifikke læringsvanskeligheder” en overordnet diagnose,der inkorporerer funktionsnedsættelser, der påvirker den akademiskepræstation. Snarere end at begrænse læringsvanskeligheder til særlige di-agnoser vedrørende vanskeligheder med at læse, skrive eller regne vil kri-terierne nu beskrive mangler ved generelle akademiske færdigheder. Der-til vil der være detaljerede angivelser i forhold til områder vedrørendelæse-, skrive- og regnevanskeligheder. Argumentet er, at klassifikationenskal være mere praksisorienteret. Ydermere påpeger DSM’s arbejdsgrup-pe, at selvom termer som dyskalkuli, dysleksi (ordblindhed eller læsse-vanskeligheder) og dysgrafi (skrivevanskeligheder) stadig bliver anvendt,indgår termerne ikke hverken i den amerikanske skolelov eller -retningslinjer (www.dsm5.org)7.Det bliver interessant at se, om ICD-11 vil lægge sig op adDSM-5, og i så fald, hvilken betydning det vil have for både praksis ogforskning på feltet. Vi har i det følgende samlet et par overvejelser fra deeksperter, vi løbende har haft kontakt med. Eksperterne er nævnt mednavn i forordet, men vi har valgt at anonymiserer dem i rapporten,hvormed de vil blive refereret til som ”eksperter”.6. DSM har en afgørende praktisk betydning i USA, da den fungerer som en universal autoritet forpsykiatriske diagnoser. Anbefalede behandlinger samt betaling af leverandører af sundhedsydel-ser bliver ofte bestemt ud fra DSM klassificeringen.7. http://www.dsm5.org/Documents/Specific%20Learning%20Disorder%20Fact%20Sheet.pdf.

En ekspert fremhæver, at det, i og med der stort set ingen prak-sis er, formentlig ikke vil give anledning til nogen særlig ændring. Denneekspert forestiller sig, at omdrejningspunktet er, at man ikke vil lave endefinition på specifikke vanskeligheder, fordi det er kompliceret at defi-nere tilstrækkelig præcist. Eksperten påpeger yderligere, at der ofte indgårfølgevanskeligheder, samt at der ofte er nuancer i de vanskeligheder, somtalblindhed kan medføre. Imidlertid påpeger eksperten, at det, at dyskal-kuli er svært at definere, ikke er det samme som at afskrive dens eksi-stens. Eksperten eksemplificerer: ”Det kan være vanskeligt at definereduften af kaffe, men vi har så gode erfaringer med duften, at det ikkevolder os besvær at konstatere, at det er kaffe. En polsk matematikersagde en gang ”jeg kan ikke identificere min kone, men jeg ved, at det erhende, når jeg ser hende”.En anden ekspert forstår paraplybegrebet ”læringsvanskelighe-der” sådan, at det omfatter elever, der er udfordret på deres arbejdshu-kommelse, hvilket kan have specifikke udtryk inden for læsning, skriv-ning og matematik. Denne ekspert mener, at alle elever kan have gavn af,at der kommer fokus på arbejdshukommelse, herunder den lærendehjerne, og derfor kan undervisning, der medtænker arbejdshukommel-sens funktion være et eksempel på en inkluderende strategi.En tredje ekspert udtaler, at DSM-5 formentlig lægger sig op aden forståelse af, at dysleksi (ordblindhed) og dyskalkuli har så mange de-finitioner, at de ikke er brugbare som selvstændige diagnoser. Dog aner-kender APA, at vanskelighederne eksisterer, hvormed de inddrages i densamlede beskrivelse. Samme ekspert fremhæver denne kommentar fraAPA:”Ved at udvide den diagnostiske kategori afspejler det den sene-ste videnskabelige forståelse af tilstanden. Specifikke symptomer,såsom læsevanskeligheder, er kun symptomer. I mange tilfældepeger et symptom i retning af en samling af større vanskelighe-der. Disse vanskeligheder kan have langsigtede indvirkninger påpersonens evne til at fungere, fordi så mange dagligdagsaktivite-ter kræver beherskelse af talfakta, skrevne ord og udtryk. Tidligidentifikation og intervention er særligt vigtige. Den udvidedeDSM-5 kategori af specifikke læringsvanskeligheder vil sikre, atfærre berørte individer vil være uidentificerede, mens de detalje-rede specifikationer vil hjælpe klinikere til effektivt at målrettetilbud og behandlingsmuligheder.” (egen oversættelse).

Processen med at identificere og beskrive dyskalkuli kan opdeles i trefaser: Vi må påpege, at der er tale om en iterativ proces, som vi her be-skriver lineært:For det første har SFI’s bibliotekar udført litteratursøgning påområdet. Som udgangspunkt har bibliotekaren søgt på al forskning omdyskalkuli hos børn med vægt på litteratur fra Danmark, Sverige, Norgeog Storbritannien. Vi har særligt været interesserede i definitioner af dy-skalkuli, test for dyskalkuli hos børn i skolealderen og støtteformer. SFI’sbibliotekar har søgt på nordiske og internationale databaser, og for atsikre at litteratursøgningen var så bred som mulig, er søgningen inspire-ret af begreber og termer, vi er stødt på undervejs. Årsagen er, at der ikkealtid benyttes de samme termer om fænomenet, hvilket har været med tilat vanskeliggøre processen.BOKS 2.1Oversigt over anvendte databaser og søgeord.DatabaserDIVA, EBSCO, Worldcat, ERIK, APA,Web of scienceSøgeordTalblindhed, Dyskalkuli, Dyscalculia,Dyskalkulie, Acalculia, Matematikvans-keligheder, Matematikkvansker, Special needseducation in mathematics, LD in math, LD inapplied math skills, Math disabilities,number sense.

bøger kan gå tabt som kilder, fordi de ofte ikke er igennem en peer re-view-proces. I dette tilfælde har vi derfor også medtaget konferencepapi-rer og bøger. Undervejs har vi også været opmærksomme på kvalitets-krav og kildekritiske krav, som ligeledes har bidraget til at begrænse an-tallet af søgeresultater. Vi har primært søgt på nyere litteratur fra år 2000og frem, imidlertid har vi også inddraget ældre materiale, hvis det harhaft relevans for projektets formål, fx i forhold til den historiske udvik-ling på området.Denne metode kunne imidlertid ikke spille den hovedrolle, denville indtage på mange andre felter, da det som nævnt drejer sig om etmeget lidt udforsket område. Det meste materiale har vi derfor fremskaf-fet gennem identifikation af eksperter i Danmark, Sverige, Norge ogStorbritannien. Eksperterne har vi identificeret sideløbende med og påbaggrund af litteratursøgningen. De eksperter, vi identificerede i Dan-mark, er blevet kontaktet per mail og har på den måde haft mulighed foraktivt at anbefale hinanden og andre med relevans for emnet.I anden fase har vi fremskaffet artikler, bøger, konferencemate-rialer, oversigter over forsknings- og udviklingsprojekter samt testmateri-aler fra de forskellige identificerede kilder. Materialerne er blevet sorteretog tematiseret. Blandt andet har vi lagt vægt på, at det var nyere litteratur,og vi har derfor frasorteret litteratur før år 2000 i de fleste tilfælde. Der-udover har vi så vidt muligt frasorteret litteratur, der behandler andretyper matematikvanskeligheder uden at komme ind på dyskalkuli. Vedfund af relevant litteratur har vi søgt på anden litteratur af samme forfat-ter(ere) og sekundærlitteratur, som teksterne henviser til. Vi har i sorte-ringsfasen været opmærksomme på, om der er enkelte forfattere, der of-tere bliver refereret til end andre, og på den måde ladet forfatterne anbe-fale hinanden.For det tredje har vi på baggrund af ovenstående udformet enoversigt over, hvilke temaer der bliver forsket i, herunder hvilke definiti-oner der anvendes, og dertil hvilke resultater der er nået, og hvilke testder eventuelt er udviklet, samt hvilke støtteformer der bliver anvendt.Det vil sige, at oversigten består af tre kortlægninger; en af definitioner,en af test og en af støtteformer. Endelig har vi opsummeret de vigtigsteresultater i et skema, vedlagt som bilag 1.Undervejs i processen er eksperter i Danmark blevet inddragetog har bidraget med deres indsigt i og erfaringer på området og løbendekommenter et på udkast af rapporten.

Selvom det er lidt utraditionelt, har vi på baggrund af rapportensformål valgt at tilføje al litteraturen. Det vil sige, at udover den litteratur,vi anvender i rapporten, indeholder litteraturlisten stort set al den littera-tur, vi har fundet frem og sorteret, som har vist sig at omhandle emnet.Denne lidt utraditionelle litteraturliste har vi valgt dels på baggrund af, atvi af gode grunde ikke har haft mulighed for at nå hele vejen omkring allitteraturen. Dels fordi vi formoder, at listen kan være et positivt bidragtil det videre forløb med testudviklingen.

Dyskalkuli-området er præget af mange og meget forskellige discipliner.Det strækker sig fra udviklingspsykologi, kognition og neurologi til di-daktik, specialpædagogik og sociologi. De forskellige fagområder prægerhver især området, men de forskellige fagsproglige termer og den mang-lende kommunikation faggrupperne imellem kan være med til at skabeforvirring omkring fænomenet dyskalkuli. Den følgende beskrivelse afudviklingen af forskningen på området er primært baseret på Lunde(2012) og Magne (2006), idet de begge har bidraget med brugbare be-skrivelser af den historiske udvikling inden for området med vægt påforskning.Den medicinske forskning har været det første område til atpræge teorier om dyskalkuli, og denne forskning indeholder fortsat syns-punkter af stor betydning. I starten af 1900-tallet begyndte neurologer atinteressere sig for personer med skader i venstre hemisfære (hjernehalv-del), da det viste sig, at disse personer havde store vanskeligheder med tal,uden at der viste sig sproglige forstyrrelser. Med denne interesse opstodteorien om et særligt regne- eller talcenter i hjernen. Teorien blev afvistaf andre (heriblandt Alexander Luria8), der mente, at der var tale om me-re komplekse forbindelser, og at vanskeligheder med tal skal findes i for-skellige regioner i hjernen (Lunde, 2012). Dette er fortsat en aktuel debat.Interessen for sammenhængen mellem matematik og sprog harogså medført forskning i læsevanskeligheders indflydelse på matematik-8. Alexander Luria var en russisk psykolog og læge. Han er ofte omtalt som neuropsykologiensgrundlægger. Luria er især kendt for sit arbejde under 2. verdenskrig, hvor han ledede det førsterehabiliteringshospital. Han har senere udgivet flere bøger og artikler om rehabilitering, hvor hanprimært beskæftiger sig med hjernen.

vanskeligheder. Sammenhængen mellem sprog- og talvanskeligheder erdog fortsat uafklaret.Psykiateren Ranschburg fremsatte nogenlunde samtidig en teoriom, at regning var en intellektuel aktivitet, som derfor måtte være knyttettil den enkeltes evner. Han skelnede mellem lavt præsterende og normaleelever. Lavt præsterende elever mente han var mentalt tilbagestående,mens normale elever havde en anden årsag til deres regnevanskeligheder.Ranschburgs løsningsforslag var god undervisning med vægt på logiskforståelse (Lunde, 2012).Med behaviorismen blev der imidlertid sat fokus på færdighederog små læringsskridt snarere end på intellektuelle evner. Her var stimuli-respons-tænkningen (”law of effect”)9dominerende (også kendtsom ”belønning og straf”), men med dårlige resultater (Lunde, 2012).Teorien kunne konstatere, at stimuli (eller handling) koblet med en hen-holdsvis positiv eller negativ respons med stor sandsynlighed vil medføre,at stimuli (eller handlinger) med tiden henholdsvis vil blive gentaget ellervil aftage.Omkring 1920 begynder interessen for regnevanskeligheder atvokse frem i Europa. Den første til at udføre et systematisk studium afregnevanskeligheder var den svenske neurolog Henchen i 1920. Henchenfokuserede på basale regnefærdigheder, hvor han knyttede særlige van-skeligheder til neurologiske defekter. Han anvendte i den forbindelsetermen ”alkalkulia” (Magne, 2006). I dag bliver begrebet alkalkulia an-vendt om regnevanskeligheder, som er opstået på grund af hjerneskade.I slutningen af 1960’erne satte svenske Oluf Magne som denførste fokus på psykologiske og sociale faktorer i forbindelse med regne-vanskeligheder. Magne er den i Norden, der først og fremmest har be-skæftiget sig med de vanskeligheder, der er knyttet til læring af matematik(Lunde, 2012). Magne publicerede senere (2001) en meget omfattendebibliografi, hvor han systematiserede omkring 5.000 forskningsdokumen-ter om dårlige matematikpræstationer, hvoraf de første dokumenter erfra 1886.Den schweiziske udviklingspsykolog Piaget blev for alvor kendt i1960’erne. Piaget var interesseret i børns generelle kognitive færdighederog arbejdede blandt andet med børns forståelse af talmængder. Han harblandt andet påpeget børns stigende forståelse af, hvorfor to mængder9. Se fx Lloyd Morgan, Edward Thondike, John B. Watson og Ivan Pavlov, som alle har været enga-geret på området og skrevet et utal af bøger.

kan have samme talstørrelse samt den form for manipulation med tal ogmængder, som påvirker talstørrelsen. Piaget var muligvis en af de førstetil at påpege, at talforståelse betyder, at man formår at se bort fra irrele-vante forhold ved tælling af en mængde (Butterworth, 1999; 2008).I 1970’erne var især den tjekkiske Ladislav Kocs populær. Kocser ophavsmand til begrebet ”udviklingsmæssig dyskalkuli” (developmen-tal dyscalculia), hvormed han opfatter dyskalkuli som et arveligt fæno-men. Senere har Ruth Shalev forsket i regnevanskeligheder og arvelighed.Han rapporterer 10 gange hyppigere forekomst af regnevanskeligheder ibestemte familier end i populationen generelt (et resultat, der senere harværet vanskeligt at verificere).I 1980’erne kom der mere fokus på informationsbearbejdning iforbindelse med læringsvanskeligheder. Her handlede det mere om stra-tegier for effektiv opgaveløsning og vanskeligheder hermed.10SnorreOstad fra Norge har senere gennemført omfattende forskning i regne-vanskeligheder. Han har især arbejdet med teorier om informationsbear-bejdning og strategier til kunne hente aritmetiske informationer (Lunde,2012).Der er således flere fagspecifikke områder, der i tidens løb harbeskæftiget sig med regnevanskeligheder. Området er derfor også prægetaf mange forskellige tilgange, herunder valg af begreber, definitioner ogkriterier, hvilket afspejler sig i litteraturen. Den store variation i forholdtil begrebsvalg og definition har netop været en af de største udfordrin-ger både for området og for udformningen af denne kortlægning.

BEGREBER OG DEFINITIONERDette kapitel består af en kortlægning af definitioner af dyskalkuli medsærlig vægt på viden fra Danmark, Sverige, Norge og Storbritannien.Kapitlet har fokus på de anvendte definitioner, hvorvidt defini-tionerne opererer med flere typer af dyskalkuli, hvordan disse typernærmere er karakteriseret, samt hvilke færdigheder det drejer sig om. Vivil starte med at se på de forskellige begreber, der bliver anvendt medhenblik på at give et billede af, hvordan begrebsvalg kan påvirke definiti-oner af talblindhed. De mest fremtrædende begreber vil blive nævnt, ogenkelte af disse vil også blive præsenteret løbende.11Afslutningsvis vil vi samle op på, om der er områder, hvor derhersker en vis konsensus i forhold til, hvad dyskalkuli er og på det grund-lag give et bud på en konkret definition, som vi kan anvende i det videreforløb.

Helt grundlæggende er der hverken konsensus om, hvilket begreb derskal anvendes, eller hvad et sådant begreb skal dække over. Der er dertilstor variation med hensyn til, i hvor høj grad forskellige studier på områ-det afgrænser det valgte begreb. Det vil også sige, at det kan være sværtat adskille studier af dyskalkuli fra studier, som undersøger en udvidetgruppe af elever med matematikvanskeligheder, hvilket er med til at ska-be forvirring omkring fænomenet.Den officielle betegnelse for talblindhed er ”specifik regnevan-skelighed” eller ”dyskalkuli”12, som det står i WHO’s ICD-10. Dyskalku-li-begrebet er ikke så anvendt i Danmark og bliver primært brugt i inter-nationale sammenhænge. I daglig tale bruger vi ofte betegnelsen ”tal-blindhed” i Danmark. Men også bredere betegnelser som ”matematik-vanskeligheder” og ”regnehuller” fremgår ofte i litteraturen og endda ihøjere grad end ”talblindhed”. I international sammenhæng støder viogså på betegnelserne udviklingsmæssig dyskalkuli (developmentaldyscalculia)13, aritmetisk læringsvanskelighed (arithmetic learning disabili-ty)14, matematisk funktionsnedsættelse (mathematical disability)15, blotfor at nævne nogle eksempler.Som nævnt hersker der usikkerhed på dyskalkuli-området i for-hold til begrebsvalg, definition, test, antal personer, det drejer sig om,årsagsforklaringer samt relevante interventioner. I nogle tilfælde er derendda uklarheder omkring eksistensen af fænomenet. Denne eksistens-debat er dog ikke understøttet af forskningen.16Nogle anser dyskalkulifor at være et paraplybegreb, der dækker over en række tilstande, der for-årsager specifikke regnevanskeligheder. Nogle mener også modsat, atspecifikke regnevanskeligheder forårsager dyskalkuli, selvom begreber-ne ”dyskalkuli” og ”specifikke regnevanskeligheder” officielt dækkerover det samme fænomen (jf. WHO’s ICD-10). Andre mener, at termendyskalkuli skal begrænses til blot at beskrive én enkelt mangel – nemligtalfornemmelse. Andre igen mener ikke, at det giver mening at beskæfti-ge sig med så snævert et begreb eller begrebsforståelse, men at vi bør12. Dyskalkuli er sat sammen af et græsk forled og et latinsk efterled og betyder mangelfuld regne-evne.13. Fx Shalev & Gross-Tsur, 1993; Temple, 1997;Kocs, 1970.14. Fx Geary & Hoard, 2001; Koontz & Berch, 1996; Shafrir & Siegel, 1994.15. Fx Geary, 1993.16. Se fx Lunde (2006; 2012); Lundberg & Sterner (2009); Johansen (2003).

anvende en bredere definition, som også indbefatter andre vanskelighe-der, der er relateret til matematik eller matematiske færdigheder.I litteraturen er det mest anvendte begreb ”matematikvanske-ligheder”. Oluf Magne er den i Norden, der først og fremmest har be-skæftiget sig med de vanskeligheder, der er knyttet til læring af matematik.Han påpeger, at der findes over 50 forskellige diagnostiske betegnelserfor matematikvanskeligheder17(Magne, 1998; Lunde, 2012). Vi antager,at dyskalkuli indgår i flere af disse betegnelser.Bötger m.fl. (2013) påpeger, at begrebet matematikvanskelighe-der, og måden det bliver anvendt på, ikke er optimalt. Ifølge Bötger m.fl.har ordet ”vanskeligheder” negative associationer. Med dette ord er derikke længere fokus på, at det kun er inden for specifikke områder, at van-skelighederne opstår. Dertil finder Bötger m.fl., at måden, somdet ”matematikvanskeligheder” bliver anvendt på, er problematisk. Defremhæver det problematiske i, at tilstanden forekommer statisk, nårbørnene omtales som elevermedmatematikvanskeligheder snarere endeleverimatematikvanskeligheder.Bötger m.fl. (2004) og Lindenskov & Weng (2004, 2005) frem-hæver endvidere, at begrebet ”dyskalkuli” er for snævert, da det ikke kanindfange aktuelle samfundsmæssige og individuelle problemer med tal-og matematiklæring. De foretrækker begrebet ”regnehuller”, som de me-ner er mere dækkende og i praksis mere anvendeligt. Med begrebet ”reg-nehuller” er der netop fokus på vanskeligheder inden for bestemte af-grænsede områder, hvor ”huller” refererer til, at der er noget udenomhullerne, der ikke er problematisk. Desuden mener de, at begrebet ”reg-nehuller” refererer til, at det er muligt at lokalisere disse huller og entenudfylde dem eller finde en vej udenom hullerne. Det vil sige, at udgangs-punktet ikke er eleven, men de vanskeligheder eller huller eleven møder.Lunde (2001, 2012) anvender begrebet ”matematikmestring”, dahan mener, at det er vigtigt at fokusere på elevens læringspotentiale. Hanhenviser i den forbindelse også til Troels Lange. På samme måde somBötger m.fl. taler Lange ikke om elever, somharmatematikvanskelighe-der, men somer imatematikvanskeligheder. Dette, mener Lunde (ogformentlig også Bötger m.fl.), kan ændre perspektivet, således at fokusikke alene er på elevens eller individets ”defekter”. Lunde (2012) ogMagne (2004) omtaler desuden matematikvanskeligheder som et sam-mensat fænomen, der opstår i et samspil mellem flere forhold.17. Her indgår over 4.000 artikler om emnet.

Magne (1958) har tidligere anvendt betegnelsen dyskalkuli, i rap-portenDyskalkuli bland folkeskoleelever,men han har sidenhen anvendtbredere betegnelser. Med henblik på at fokusere på omfanget og sættefokus på, at det drejer sig om de elever, der er lavt præsterende i matema-tik, foreslog Oluf Magne i 1990’erne betegnelsen ”dysmatematik”. Ordetskal referere til matematikrelaterede vanskeligheder og inkluderer beteg-nelser som matematikvanskeligheder og specifikke matematikvanske-ligheder (dyskalkuli). Betegnelsen dysmatematik er kun blevet anvendt ibegrænset omfang. I de senere år har han argumenteret for betegnel-sen ”SUM-elever” (elever med Specielle Undervisningsbehov i Matema-tik). Argumentet er, at betegnelsen ikke er så defektpræget og samtidigmeget præcis ved, at den betegner behovet for tiltag. Magne søger at gøreop med det traditionelle perspektiv, hvor matematikvanskeligheder erplaceret hos den enkelte elev, hvilket han mener, at diagnosen dyskalkulier et eksempel på. Han anser vanskeligheden som en forstyrrelse mellemeleven og dets sociale og fysiske omgivelser (Magne, 1994, 2001, 2004;Lunde, 2012).Butterworth (2008) understreger, at dyskalkuli tydeligt må adskil-le sig fra matematikvanskeligheder. Han fremhæver, at matematikvanske-ligheder omfatter langt flere individer, og at deres vanskeligheder skyldesen lang række andre faktorer end dyskalkuli. Dyskalkuli omfatter en me-get lille gruppe mennesker, og skyldes en specifik mangel, hvilket vi vilkomme nærmere ind på senere i dette kapitel. Han anvender selv begre-bet ”dyskalkuli” eller ”udviklingsmæssig dyskalkuli” (developmentaldyscalculia). Sidstnævnte betegnelse er især inspireret af Ladislav Kocs.Butterworth påpeger, at det let kan føre til forvirring, når forskere an-vender samme eller tilsvarende terminologi som fx ”matematikvanske-ligheder” eller ”matematisk funktionsnedsættelse” i forbindelse med ”dy-skalkuli”, særligt hvis der ikke er en tydelig skelnen.Lunde (2003) påpeger fx på baggrund af en undersøgelse af PPT(Pædagogisk-Psykologisk Tjeneste – det norske PPR), at de er forsigtigemed at anvende betegnelserne dyskalkuli og specifikke regnevanskelighe-der. Årsagen er, at PPT er usikre på betegnelsernes betydning. Halvdelenaf kontorerne mener, at betegnelserne dækker over det samme fænomen,mens 30 pct. mener, at dyskalkuli er mere alvorligt. Dertil ser der ifølgeLunde ud til at være en teoretisk forståelse af matematikvanskelighed,som en læringsvanskelighed med klare kriterier (Lunde, 2003).

Groft opdelt findes der to overordnede holdninger til definiti-onsformer knyttet til begrebsvalg inden for området. På den ene side erden snævre forståelse, dyskalkuli, som bygger på princippet om, at detskal være en specifik vanskelighed – problemer med tal. På den andenside findes den brede forståelse (fx matematikvanskeligheder eller regne-huller), hvor fokus i højere grad er på samspillet mellem eleven og den-nes omgivelser fx undervisningsmetoden, forholdet til læren og klasse-kammeraterne samt forhold uden for skolen. De fleste eksperter, som vihar haft kontakt med, anfører – i overensstemmelse med en del af littera-turen, at matematikvanskeligheder er et bredt begreb, der groft opdeltdrejer sig om tre typer af årsager: 1) Problemer med tal, 2) Problemermed sprog og 3) Manglende hverdagserfaring. Af disse tre årsager dæk-ker den første (problemer med tal), den specifikke tilstand – dyskalkuli.Begrebet matematikvanskeligheder er derfor alt for bredt et begreb set iforhold til formålet med denne oversigt og det videre forløb med testud-viklingen. Vores fokus i denne rapport er på dyskalkuli, forstået somspecifikke problemer med tal.De mange og forskellige begreber og anvendelser kan være etudtryk for, at området er præget af mange og forskellige fagområder, her-iblandt udviklingspsykologi, kognition, neurologi, didaktik, specialpæda-gogik og sociologi. Forskere inden for de forskellige områder har megetforskellige mål med deres forskning, og en del af dem har ingen erfaringmed praksis. Et overordnet problem er en mangel på kommunikationfaggrupperne imellem. Dertil kommer, at forskerne ikke taler sammesprog (Lunde, 2012, 2003). Da begreberne tager udgangspunkt i forskel-lige traditioner og dermed forskellige perspektiver i forhold til begrebs-valg og -anvendelse samt årsagsforklaringer og definitioner, skaber det isig selv forvirring på området.I det følgende afsnit skal vi se nærmere på, hvordan man ud fraforskellige perspektiver omtaler dyskalkuli i litteraturen.

Dyskalkuli har betegnelsen 81.2 i ICD-10, og er derfor i katego-rien af specifikke udviklingsforstyrrelser af skolefærdigheder, indlærings-forstyrrelse.18ICD-10 anvender betegnelsen specifik regnevanskelighed(dyskalkuli) og definerer det således:… tilbagestående regnefærdigheder, som ikke skyldes mental re-tardering eller mangelfuld skolegang. Regnevanskelighederneomfatter manglende evne til at beherske basale regnefærdig-heder, såsom addition, subtraktion, multiplikation og divisionsnarere end mere abstrakte matematiske færdigheder i algebra,trigonometri, geometri og komplekse beregninger.Ifølge WHO’s ICD-10, forekommer dyskalkuli hos normaltbegavedemennesker. Er der fx tale om en person, der har problemer med tal ogsamtidig har en IQ, der er lavere end normen, er der således ikke taleom ”specifik regnevanskelighed”. Definitionen inkluderer udviklings-mæssig akalkuli19, udviklingsmæssig regneforstyrrelse og udviklingsmæs-sig Gerstmanns syndrom.20WHO’s definition ekskluderer erhvervet reg-neforstyrrelse (fx på baggrund af erhvervet hjerneskade, fx erhvervetakalkuli), regnevanskeligheder ved læse- og staveforstyrrelser eller regne-vanskeligheder ved utilstrækkelig undervisning. Som det ser ud nu, erWHO’s definition ikke yderligere konkret i forhold til, hvilke konkretekriterier der skal være opfyldt. Dette efterlader det konkrete indhold afdyskalkuli åbent for fortolkning.Det Britiske undervisningsministerium anvender en lidt merepræcis definition af dyskalkuli. Det er denne definition, de britiske for-skere på området tager udgangspunkt i (fx Butterworth, Emerson &Babtie, Hannell m.fl.). Det Britiske undervisningsministerium definererdyskalkuli således:En tilstand, som påvirker evnen til at tilegne sig basale regnefær-digheder. Mennesker med dyskalkuli kan have vanskelighederved at forstå enkle begreber om tal, kan mangle en intuitiv for-nemmelse for tal og have vanskeligheder ved at lære tal regler ogprocedurer. Selv hvis de når frem til svar, som er korrekte eller18. I ICD-10 betegnes kategorierne F80-F89 ”psykiske udviklingsforstyrrelser”, hvorunder F81kategorien betegnes ”specifikke udviklingsforstyrrelse af skolefærdigheder, indlæringsforstyrrel-ser”.19. Alkalkuli er enerhvervetdefekt i udførelse af simple regnestykker20. Gestmanns syndrom er en hjernelidelse hos voksne

bruger korrekte metoder, så kan de gør dette mekanisk og udenat føle sig sikre.21(UK Department for Education and Skills(DfES), 2001. Egen oversættelse).Den Britiske definition er ligeledes åben for fortolkning, og den beskri-ver heller ikke, hvad der ligger bag vanskelighederne (Butterworth, 2003).Flere eksperter påpeger, at WHO’s ICD plejer at lægge sig op adden amerikanske klassifikation DSM (Diagnostic and Statistical Manualof Mental Disorders). I den fjerde udgave af klassifikationen fra APA(DSM-4) anvender man følgende diagnostiske kriterier for matematiskfunktionsnedsættelse (mathematics disorder):Matematiske færdigheder, som er individuelt målt i administrati-ve standardiserede test, fremstår substantielt under det forvente-de – personens kronologiske alder, målte intelligens og alders-svarende uddannelse taget i betragtning – hvilket har signifikantindflydelse på akademiske præstationer eller dagligdagsaktivite-ter, der kræver matematiske færdigheder.22(APA, 1994, afsnit315.1. Egen oversættelse).Den amerikanske beskrivelse af diagnostiske kriterier for matematiskfunktionsnedsættelse lægger vægt på elevens score på standardiseredetest. Standardiserede test tester som regel en lang række færdigheder,hvorefter resultaterne lægges sammen til en total score, som skal beskriveelevens matematiske færdigheder. Imidlertid kan der være flere årsager til,at en elev scorer højt eller lavt på en standardiseret test, hvilket hverkendefinitionen eller en standard matematiktest tager højde for.23I den netop udkomne (maj 2013) femte version af DSM (DSM-5)er specifikke vanskeligheder imidlertid helt afskaffet til fordel for en ud-videlse af kategorien ”læringsvanskeligheder”. Kriterierne vil nu beskrivemangler ved generelle akademiske færdigheder og give detaljerede angi-21. ”A condition that affects the ability to acquire arithmetical skills. Dyscalculic learners may havedifficulty understanding simple number concepts, lack an intuitive grasp of numbers, and haveproblems learning number facts and procedures. Even if they produce a correct answer or use acorrect method they may do so mechanically and without confidence.” (Butterworth, 2003: side3).22. “Mathematical ability, as measured by individually administered standardized tests, is substantial-ly below that expected given the person’s chronological age, measured intelligens, and age-appropriate education, which significantly interferes with academic achievement or activities ofdaily living that require mathematical ability” (APA, 1994, afsnit 315.1 i Butterworth, 2003).23. Se mere om test i kapitel 4.

velser i forhold til områder vedrørende læse-, skrive- og regnevanske-ligheder. APA’s hensigt er at øge den diagnostiske præcision, og at denmere effektivt skal være målrettet praksis. I overensstemmelse med dengenerelle udvikling i medicinske diagnoser er APA’s definition løsrevetfra en teoretisk og en begrebsmæssig forståelse af mekanismer og aleneknyttet til empiriske eller praktiske procedurer til erkendelse af fænome-net24.Når vi ser på de officielle definitioner og kriterier, såsom deovennævnte, vedrører dyskalkuli overordnet set evnen til at erhververegnefærdigheder. Og overordnet set opfattes personer med dyskalkulisom personer, der ikke følger den normale faglige udvikling. De kriterier,som er beskrevet, er imidlertid ikke tilstrækkeligt konkrete, og de efterla-der fortsat det specifikke indhold af dyskalkuli åbent for fortolkning. Viantager, at den manglende præcision i de officielle definitioner kan væreen af forklaringerne på, at en stor del af de personer, der beskæftiger sigmed området, anvender andre definitioner. En anden forklaring ligger ide forskellige faglige tilgange, der bliver taget udgangspunkt i, hvilket vi inæste afsnit skal se nærmere på. I vores omtale af forskning og artiklervil vi primært anvende de betegnelser, som forfatterne selv anvender.FORSKELLIGE PERSPEKTIVER

met, hvormed de knytter vanskelighederne til den kognitive produktion,og hvordan informationer bearbejdes i hjernen.Da det viste sig, at mennesker med skader i hjernens venstrehemisfære havde store vanskeligheder med tal, men ikke sproglige for-styrrelser, begyndte neurologer allerede i starten af 1900-tallet at interes-sere sig for problemer med tal eller regnevanskeligheder. Peritz fremsattesenere teorien om et regnecenter i hjernens venstre side. Andre, fx Luria,afviste Peritz’ teori og mente, at årsagen til vanskeligheder med tal ogregning skulle ligge i forskellige regioner i hjernen (Lunde, 2012). Oven-stående er en debat, der fortsat er aktuel. Der er dog enighed om, at van-skeligheder kan hænge sammen med neurologiske defekter.Blandt andre taler Brian Butterworth, britisk professor i kognitivneuropsykologi, fx om ”den matematiske hjerne” eller ”hjernens talmo-dul”. Udgangspunktet er en forståelse af, at mennesket har en medfødtevne til at erkende og håndtere små antal allerede fra spædbarnsstadiet,idet det er påvist, at selv spædbørn kan skelne mellem op til fire genstan-de. Teorien er, at mennesket er født med evnen til at opfatte to talsyste-mer. Det ene er evnen til at registrere små antal uden at tælle (op til firegenstande). Det andet er evnen til umiddelbart at skelne mellem forskel-lige antal (Butterworth, 2003, 2005, 2008; Berteletti m.fl., 2010).26Lig-nende evner er også fundet hos dyr27, fx aber, mus, fugle og fisk, hvilketkan tyde på, at talforståelse i en vis udstrækning er medfødt (Butterworth,2003).Ifølge Butterworth (2003, 2005) er dyskalkuli et specifikt pro-blem med at forstå numeriske koncepter, særligt talmængder. Han frem-hæver desuden, at hjerneforskning indikerer, at der findes en formfor ”tal-modul” i isselappen i hjernen, som er specialiseret i håndtering afnumeriske repræsentationer. Dertil indikerer forskning yderligere, at isse-lappen ikke er udviklet normalt hos børn med dyskalkuli. Butterworth(2003) anerkender imidlertid også sprogets og hukommelsens rolle i for-bindelse med indlæring af tal og regneprocesser. Når det drejer sig omdyskalkuli, understreger han dog, at sprog- og hukommelsesproblemerskal være direkte knyttet til tal og regning. Butterworth mener derfor, at26. Se evt. også K. Wynn (1992): ”Addition and Subtraktion by Human Infants”. Nature, 358, s.749-751.27. Butterworth henviser til: Bosen, 1993; Boysen & Capaldi, 1993; Brannon & Terrace, 1998, 2000;Hauser, MacNeilage & Ware, 1996; Pepperberg, 1987; Washburn & Rumbaugh, 1991. James Gil-lum har i øvrigt også udarbejdet en ”planche” over dyskalkuli, hvor emnet indgår:http://prezi.com/sd-q9fynm7vp/dyscalculia/.

Numeriske fakta (number facts). Basalt set drejer det sig om alle tal-forhold for hvert af tallene fra 1-10 – fx at tallet 5 kan repræsentereen mængde, som indeholder 5 genstande eller 2 mængder, som in-deholder henholdsvis 4 og 1 genstand eller 3 og 2 osv. Dette kaldesogså talbindinger (number bonds), fx at en binding af 5 udgør 3 plus2. En person med dyskalkuli har en simpel forståelse af tallet og for-står ikke, at tal kan udgøres af forskellige kombinationer.Taloperationer (numerical operations). Her drejer det sig om basalehandlinger, når tal operationaliseres: addition, subtraktion, multipli-kation og division. Personer med dyskalkuli vil have svært ved atforstå begrebet om de fire handlinger, og ofte kan de ikke huskeprocedurerne for at udføre beregningerne.Positionssystemet (place value and the principle of exchange): Herhandler det om, hvad et tal repræsenterer eller tallets kodning. Dethandler om at forstå positionssystemet og at kunne operere i det.Det vil sige en forståelse af, at de 10 cifre (0-9) er nok til at repræ-sentere ethvert antal. Cifrets værdi vil afhænge af cifrets placering idet samlede tal (fx at sætte 2 og 9 sammen til 29 eller 92).

Emerson & Babtie (2012) pointerer, at det at være talkyndig betyder, atindividet forstår, hvad et tal er, og hvordan tal relaterer sig til hinanden.Det at tælle vil derfor fordre basal talkyndighed.I forbindelse med et udviklingsprojekt i Nordjylland forsøgerprojektgruppen, herunder Henrik Skovhus, at byde ind med en definition.Med projektgruppens definition af dyskalkuli er deres ønske at betone, atdyskalkuli er en afgrænset funktionsnedsættelse, der er begrundet neuro-genetisk.Dyskalkuli er en funktionsnedsættelse af neuro-genetisk oprin-delse, der skyldes medfødte vanskeligheder med den intuitiveforståelse af mængder og antal. Dyskalkuli er kendetegnet vedvanskeligheder med talforståelse og nedsat evne til at tilegne siggrundlæggende matematiske færdigheder og procedurer. Vanske-ligheder er ofte uventede set i forhold til andre kognitive og ind-

Andre forskere læner sig op ad Ladislav Kocs (1970), der mener, at dy-skalkuli er et arveligt fænomen. Kocs er ophavsmand til begrebet ”udvik-lingsmæssig dyskalkuli” (developmental dyscalculia). Kocs påpeger, atdyskalkuli drejer sig om særlige kognitive funktioner, der ikke har udvik-let sig på normal vis, hvilket senere fører til regnevanskeligheder. Hanfandt senere ud af, at nogle personer fik regnevanskeligheder på grund afen given situation og ikke medfødte egenskaber, hvilket hante ”pseudo-dyskalkuli”.28Kocs’ definition fra 1970 lyder således:En strukturel forstyrrelse af matematiske evner, der har sin op-rindelse i en genetisk eller medfødt lidelse i de dele af hjernen,der er det direkte … psykologiske fundament til modningen afmatematiske evner, der er passende i forhold til personens alder,uden at der samtidig er generelle mentale funktionsforstyrrelser29(Kocs, 1970 i Lunde, 2012. Egen oversættelse).I forlængelse af Kocs’ forskning er der forskere, der blandt andet harundersøgt dyskalkuli og arvelighed hos tvillinger. Kadosh & Walsh (2007)fremhæver, at selvom læringsmiljø spiller en rolle i forhold til regnefær-digheder, så tyder forskning på, at dyskalkuli kan være arveligt betinget.De påpeger, at Alarcon med fleres tvillingeundersøgelse fra 1997 viser, athvis én tvilling har dyskalkuli, så er der 58 pct. sandsynlighed for, at denanden enæggede tvilling også har dyskalkuli. Ved toæggede tvillinger erden tilsvarende sandsynlighed 39 pct. Kadosh & Walsh understreger, atdyskalkuli ikke er det samme som at være dårlig til matematik. De påpe-ger, at forstyrrelsen er forbundet med individets manglende evne til at28. Butterworth har også tage begrebet ”pseudo-dyskalkluli” til sig.29. ”A structural disorder of mathematical abilities that has its origin in a genetic or cengenital disor-der of those parts of the brain that are direct … psychological substrate of the maturation ofmathematical abilities adequate to age, without a simultaneous disorder of general mental func-tions”.

forstå tal og talmængder. Ifølge Kadosh & Walsh kan dyskalkuli omfatteflere undergrupper med forskellige karakteristika, fx mangler og besværved forskellige færdigheder, såsom automatisk bearbejdning af talinfor-mation, evnen til at se sammenhængen mellem symboler og størrelser,evnen til at genkalde talregler samt effektivt at udføre regneprocedurer(Kadosh & Walsh, 2007).Lundberg & Sterner (2009) fremhæver ligeledes Alarcon medfleres tvillingeundersøgelse fra 1997. Lundberg & Sterner fremhæverendvidere Shalev, Manor, & Gross-Tsurs familieundersøgelser fra 2001.Familieundersøgelsen viser, at halvdelen af alle søskende til et barn meddyskalkuli også selv er ”påvirkede” af dyskalkuli. Dette betyder, at sø-skende til et barn med dyskalkuli har 5-10 gange større sandsynlighed forat have dyskalkuli end andre børn. Lundberg & Sterner pointerer, atforskning med fokus på arvelighed har været betydeligt mere intensiv,hvad angår dysleksi (ordblindhed). De påpeger, at forskningen viser, atmere end 50 pct. af variationerne af læsevanskeligheder kan forklares udfra variationer i arveanlæg. I forhold til dysleksi har forskningen identifi-ceret seks kromosomer med afvigende gener, hvilket spiller en afgørenderolle. Lundberg & Sterne påpeger, at forskningen endnu ikke så langtfremme i forhold til dyskalkuli. Samtidig fremhæver de, at gener ikke ale-ne er afgørende, men at andre faktorer også spiller ind.I en dansk kontekst indikerer CSV’s projekt, at der er en arveligfaktor, da det viser sig, at flere i familien ofte har indlæringsvanskelighe-der. Årsagerne er dog ikke helt afklarede (CSV, 2010). I forhold til dy-skalkuli og arvelighed er det imidlertid vanskeligt at afgøre, om der er taleom miljøpåvirkninger eller arveanlæg.Sjöberg (2008) mener, at dyskalkuli kan være en forklaring påmatematikvanskeligheder blandt børn, men at det langt fra er hovedfor-klaringen. Sjöberg & Nyroos (2007) påpeger, at en medicinsk-neurologisk tilgang og diagnosen dyskalkuli ikke alene kan forklare ele-vernes vanskeligheder. Snarere synes en række psykologiske, sociologiskeog pædagogiske faktorer at give den nødvendige forklaring. Sjöberg(2008) mener endvidere, at det er kritisabelt, at det særligt er neurologerog neuropsykologer, der har fortrinsret til fortolkning på et område, der istor udstrækning har et pædagogisk fundament.Samlet set er der en forståelse af, at dyskalkuli handler om hjer-nens måde at fungere på, herunder den neurale kommunikation, og atder er en vis arvelig faktor i dyskalkuli. Det neurologiske perspektiv byg-

ger på viden om, at børn har en medfødt talfornemmelse, forstået somtal- og mængdeforståelse (eller forståelse for antal). Dyskalkuli kommeraltså til udtryk ved vanskeligheder med netop talfornemmelsen. Imidler-tid er der andre forskere, der påpeger, at denne tilgang ikke kan stå alene,idet regneprocedure også må bygge på barnets erfaringer.Mange af de eksperter, vi har været i kontakt med, påpeger, atneurologernes arbejde er meget relevant, men de fremhæver samtidig, atneurologerne ikke nødvendigvis har en realistisk forståelse af, hvorledesmatematikundervisningen foregår i praksis, og hvilke færdigheder dettekræver af børnene. Dertil fremhæver eksperter, at det at indkredse van-skelighederne ifølge neurologerne er uafhængigt af uddannelserne. Sam-tidig er det dog en didaktisk opgave at implementere viden og nå frem til,hvordan viden kan resultere i bedre undervisning.PSYKOLOGISK PERSPEKTIV

I et psykologisk perspektiv bliver dyskalkuli anset som en forstyrrelse igrundlæggende psykologiske processer. Det kan fx være manglende mo-tivation, koncentrationsbesvær, angst, herunder præstationsangst ogholdninger til faget matematik eller forskellige kognitive funktioner så-som strategier, perception, hukommelse og lignende eller sprogfærdighe-der og begrebsudvikling.Denne del af litteraturen tager afstand fra diskussionen om,hvorvidt det drejer sig om et specifikt område i hjernen, men er stadigstærkt inspireret af hjerneforskning. Her drejer det sig snarere om, hvilkekognitive processer der er centrale, og hvordan de korresponderer medhjernemekanismerne. Matematiske færdigheder er i dette perspektiv rela-teret til mere generelle kognitive funktioner. Her er der også en del over-lap til det neurologiske perspektiv. Det kan dreje sig om semantisk hu-kommelse, arbejdshukommelse eller rumsans. Det kan være svag op-mærksomhedskontrol og svag forhindring af irrelevante associationer,eller det kan være vanskeligheder med at repræsentere informationer ogmanipulere dem sprogligt (Geary, 1993, 2004; Adams & Hitch, 1997;Ostad, 2004, 2006; Butterworth & Yeo, 2004). Det vil sige, at dyskalkulivil komme til udtryk i den enkeltes strategier for fx at bearbejde små tal,hvor personen eksempelvis opfatter én genstand ad gangen og må tælle istedet for at regne (fx på fingrene), mens andre både kan opfatte en sam-ling af genstande som ét hele og samtidig opfatte en samling af genstan-de, som individuelle genstande.

Den svenske neuropsykolog Björn Adler anser dyskalkuli somen kognitiv funktionsnedsættelse på lige fod med dysleksi og ADHD.Ifølge Adler (2003) rummer dyskalkuli en masse forskellige matematik-vanskeligheder, der kan skyldes både automatiseringsvanskeligheder samtsproglige vanskeligheder og planlægningsvanskeligheder. Det primæreproblem for personer med dyskalkuli er ifølge Adler, at de har svært vedautomatisk at udvælge og hente den nødvendige information frem fx vedudregning af matematikopgaver. Han fastslår, at dyskalkuli kun omhand-ler specifikke vanskeligheder og ikke al matematikken. Adler mener des-uden, at svingende præstationer er karakteristisk for dyskalkulikere.ANGST

Angst og stress kan have negativ indflydelse på elevernes præstationer.Forenklet sagt påvirker elevens ydre miljø elevens indre miljø på en så-dan måde, at der opstår vanskeligheder (Lunde, 2006, 2012). Det kaneksempelvis dreje sig om en tilstand, hvor eleven kan have en følelses-mæssig blokering over for faget matematik fx at elevens fiasko-oplevelserved dele af matematikken kan medføre mindreværd og angst, hvilket kanhave negativ indvirkning på elevens trivsel med faget. Formentlig inspire-ret af Ladislav Kocs omtaler Adler og Grynberg dette som ”pseudo-dyskalkuli” (Adler, 2003, 2008; Grynberg, 2010). I den forbindelse kriti-serer Adler specialundervisningen. Han påpeger, at den store indsats forat afhjælpe elevens matematikvanskeligheder ved hjælp af ekstra timermed flere regneopgaver kan være med til at øge elevens dårlige selvværd,da eleven fortsat ikke kan løse regneopgaverne.Sjöberg (2006) påpeger, at flere af de elever, der indgår i hansundersøgelse, forklarer, at de føler stress og angst i forbindelsen med test.Sjöberg & Nyroos (2007) fremhæver ligeledes, at der er kommet en stig-ning i antallet af elever, der opleveler testangst i det moderne samfund.Testangst definerer forfatterne som ”en række af fænomenologiske, psy-kologiske og adfærdsmæssige reaktioner, som fremkommer som følge afbekymring for eventuelle negative konsekvenser ved dårligt testresulta-tet”. De påpeger, at under deres observationer af elever ved testning ud-viste eleverne med matematikvanskeligheder øget angst- og stressniveausammenlignet med elever uden matematikvanskeligheder. Deres krops-sprog, attitude og senere kommentarer bekræftede dette.

Chinn (2009) har også undersøgt matematikangst blandt elever iStorbritannien, hvor hans resultater viser, at mellem 2 og 6 procent afalle elever lider af matematikangst.Johnson (2004) fremhæver ligeledes, at ”blokeringer” eller angster en meget omtalt tilstand i forbindelse med matematikvanskeligheder,og de bliver i høj grad opfattet som en barriere for læring. Johnsen har isine undersøgelser fundet en sammenhæng mellem generaliseret angst ogarbejdshukommelse. Yderligere kan domænespecifik angst (fx matema-tikangst) føre til forhøjet angst. Han påpeger dog, at mekanismerne bagblokkeringerne er meget komplekse og involverer flere cerebrale syste-mer.Dyskalkuli kan i et psykologisk perspektiv forklares som en for-styrrelse i en eller flere psykologiske processer, herunder kognitive funk-tioner. Litteraturen fremhæver angst, dårligt selvværd, dårlig hukommel-se og begrebsudvikling, hvilket kan komme til udtryk i barnets strategier iforbindelse med simple regneopgaver. Vi skal påpege, at der her er man-ge overlap til det neurologiske perspektiv, særligt i forhold til hukommel-se.SOCIOLOGISK PERSPEKTIV

Sociologisk set knyttes dyskalkuli til miljøfaktorer, såsom et understimu-leret miljø, sociale afsavn eller mangler, der bevirker, at eleven ikke harerhvervet de nødvendige læringsforudsætninger, herunder konkrete erfa-ringer og sprogfærdigheder.Den britiske Sarah Wedderburn (2012) peger på den modernelivsstil. Hendes udgangspunkt er, at niveauet for regnefærdigheder blandtbriterne er faldet, hvilket ifølge Wedderburn skyldes, at vores livsstil på-virker vores indlæring og hermed vores regnefærdigheder. Hun hævder,at vi i vores hverdag konstant bliver konfronteret med matematiske op-gaver, men at noget af denne hverdagsmatematik er bortfaldet grundetvores livsstil. Wedderburn problematiserer eksempelvis det, at vi i højeregrad spiser måltider væk fra bordet og i stedet foran fjernsynet, hvilketbetyder, at vi ikke længere dækker bord og derfor ikke tæller, hvor megetservice der skal være. Hermed mindskes vores forståelse for tal ifølgeWedderburn. Hun beskriver vigtigheden af, at børn gennem opvækstenbliver præsenteret for tal, da dette er grundlæggende for deres matemati-ske forståelse og mener, at den moderne livsstil ikke har nogen positivindvirkning i forhold til dette. Wedderburn fremhæver dog, at der er for-

skel på elever, der har regnevanskeligheder (dyskalkuli) og elever, derikke har opnået et stærkt nok fundament til at forstå matematiske begre-ber.Der kan også være en forældredimension, som er med til at un-derbygge den sociale dimension. Der kan fx være frustrationer i hjemmeteller forældrene kan have en negativ holdning til matematik, hvilket kansmitte af på eleverne. For eksempel forklarer flere af eleverne i Sjöbergs(2006) undersøgelse, hvordan signaler i hjemmet påvirker deres holdningtil faget matematik negativt. Gillum (2012) lægger særlig vægt på læ-ringsmiljø og sociale faktorer, såsom forældrenes indstilling til matematik,barnets motivation og selvbillede. Han påpeger, at uddannelsespsykolo-ger både inddrager læringsmæssige og sociale aspekter, når de skal forkla-re barnets regnevanskeligheder.Lundberg & Sterner (2009) påpeger, at dyskalkuli skyldes erfa-ringsbaserede udviklingsprocesser (både arvelige og miljøbetingede). Depointerer fx vigtigheden af stimuli i før-skoletiden, så børn fra udsattemiljøer får mulighed for at starte på samme niveau som børn fra bedrestillede miljøer.30Magne (1994, 2000) fremhæver den sociale dimension i forbin-delse med den såkaldte faktorsamspilsmodel. Magne anbefaler at brugefaktorsamspilsmodellen, når undervisning til elever med matematikvan-skeligheder skal målrettes. Magne udbygger dog modellen, da han mener,at der udover stimulus og responstid (som modellen indeholder) bør væ-re en social dimension. Hans argument er, at individets indlæring altidforegår i en social situation. For eksempel bliver der i en klasse opbyggeten matematikkultur, og ud af den fremtræder forskellige former fornormer og adfærdsmønstre. Den sociale kommunikation kan derigen-nem lede til konflikter, meningsudveksling og en fælles kollektiv forståel-se. Denne sociale interaktion kan give klassen en følelse af deltagelse ogsamhørighed (Magne, 1994, 2000).Simmons & Singleton (2009) ser på sammenhænge mellem ma-tematikvanskeligheder og dysleksi (ordblindhed). De kritiserer det neuro-logiske perspektiv og særligt Butterworth for hans snævre tilgang og hanstese om, at der kun er tale om én forstyrrelse. Simons & Singleton mener,at præstationer også må være påvirket af andre kognitive færdighedersåsom fonologiske opmærksomhed og sociale påvirkninger. Forfatternefremhæver, at dysleksi har indflydelse på den matematiske udvikling,30. Se fx Duncan (2007) og Siegler & Ramani (2008).

men det varierer dog, i hvilken udstrækning dysleksi influerer på forskel-lige matematiske områder. To undersøgelser foretaget af Simmons ogSingleton viste samlet set, at de dyslektiske elevers genkaldelse af tal ogregneregler var langsommere og mere upræcis end de ikke-dyslektiskeelever. Resultaterne for tællehastighed var mere enslydende, selvom dervar en lille tendens til, at dyslektikerne talte langsommere. Studiernes re-sultater viste fx, at de dyslektiske elever havde problemer med at svarehurtigt og præcist på opgaver, der omhandlede aritmetisk information,mens de præsterede på stort set samme niveau som de ikke-dyslektiskeelever, når det vedrørte opgaver om positionssystemet. Her fremhæverSimmons & Singleton Butterworths tese om, at dyslektiske elevers ”tal-modul” (number module) er svækket. At de dyslektiske elever i Simmons& Singletons studier ikke præsterede dårligt i opgaver vedrørende positi-onssystemet burde ifølge forfatterne være tilfældet, hvis Butterworthstese var sand.Andersen (2004) fremhæver sprogets rolle for matematikindlæ-ring og advokerer for, at lærere i højere grad tænker sproglige aspekterind i matematikundervisningen. Andersen konkluderer, at elevernessproglige kompetencer, både på dansk og deres modersmål, har indfly-delse på kvaliteten af deres matematiklæring. Samtidig argumenterer hanfor at tænke på matematikken som et sprog i sig selv, hvortil han frem-hæver, at elever, der lærer matematik, er udfordret af to sprog – det dan-ske sprog og ”fremmedsproget” matematik. Hertil fremhæver han, atregneopgaver blandt andet skal fortolkes, og for at finde de korrekte løs-ningsstrategier må eleven forstå, hvad en matematisk tekst drejer sig om.Andersen påpeger, at det endnu ikke er fastlagt, hvor stor en rolle spro-get har.Johansen (2007) peger også på sprogets rolle i indlæring af ma-tematik. Johansen fremhæver norsk forskning, der viser en klar sammen-hæng mellem vanskeligheder i norsk og vanskeligheder i matematik. En-kelte norske forskere betegner matematikvanskeligheder som sprogrela-terede. Johansen fremhæver også tyske undersøgelser, der viser, at bør-nene i de første skoleår alene i matematikundervisningen skal lære mereend 500 nye ord og begreber, hvormed matematik kan betegnes som ele-vernes første fremmedsprog.Lunde (2006) fremhæver ligeledes, at sprogfærdighed er den vig-tigste forudsætning for at lære matematik, da det er ved brug af begreberog sprog, at tænkning sker og kan formidles. På den måde er sproget en

forudsætning for læring. Vanskeligheder kan blandt andet opstå, når desamme ord har forskellige betydninger i henholdsvis en hverdagskon-tekst og en matematisk kontekst (fx mængde).Inden for det sociologiske perspektiv har litteraturen især fokuspå elevens relationer og erfaringer, fx i forbindelse med hverdagssituati-oner og leg hvor matematik naturligt kan integreres. Dette indbefatterogså de sproglige kompetencer, som kan påvirke elevens læringsforud-sætninger.Det er vigtigt at pointere, at der er stor forskel på specifikke reg-nevanskeligheder og matematikvanskeligheder. Fx fremhæver et par afde eksperter, vi løbende har haft kontakt med, at der er personer som erfortræffelige til sprog, men samtidig har svært ved at gange to tal medhinanden og ikke kan klokken. Det er blandt andet disse personer vi vilkarakterisere som personer med dyskalkuli i forbindelse med denne rap-port.DIDAKTISK PERSPEKTIV

Det didaktiske perspektiv lægger vægten på undervisningen og de pæda-gogiske metoder. Det kan fx dreje sig om utilpassede eller ensidige un-dervisningsmetoder, hvor eleven oplever specifikke, alvorlige og vedva-rende regnevanskeligheder på trods af god intelligens. Dette perspektivknyttes som oftest til de ovenfornævnte perspektiver. I andre tilfældebliver der taget afstand til især det neurologiske perspektiv og den medi-cinske diagnosticering. Udgangspunktet her er, at videnskabelige debatterom definitionen og specifikation af fænomenet dyskalkuli har stor betyd-ning teoretisk set, men at det har mindre betydning i det praktiske arbej-de og for de praktiske aspekter af initiativer med elever, der har vanske-ligheder.Ifølge Engström & Magne (2004) producerer skolesystemet ma-tematikvanskeligheder på baggrund af utilpasset undervisning til elevermed behov for specialundervisning. Elever med matematikvanskelighe-der oplever, at det meste pensum, der læres i de øvre klasser, er langtover deres kompetenceniveau, hvorfor de bliver ekskluderet fra matema-tiklæringen. Forfatterne påpeger, at elever med matematikvanskelighederhøjst sandsynligt kunne opnå trinmålene, hvis der skete ændringer i un-dervisningen og læringssituationerne. Det kunne bl.a. ske ved, at man ihøjere grad organisede matematikundervisningen omkring social- oghverdagsmatematik.

Magne (2000) vil gøre op med den klassiske specialundervisning,som han ikke mener hjælper. Han kritiserer den klassiske specialunder-visning for at være indstillet på en passiv formidlingsdidaktik, hvor lære-ren blot ”fylder” eleverne med færdigheder. Magne mener, at en inddra-gelse af specialpædagogikken i stedet skal omfatte fleksible og rige lære-planer, højt kvalificerede lærere og en engagerende matematikundervis-ning med lige chancer for at udvikle kundskaber. Elevens læring er base-ret på, at eleven ”aktivt skal bearbejde” og ”frivilligt søge”. Samtidig skaleleven udvikles i og igennem et socialt netværk. Selve matematikken øn-sker Magne skal være baseret på det, han kalder ”livsmatematik”. Magneanerkender imidlertid, at der kan være tale om en neurologisk forstyrrelsei forbindelse med dyskalkuli eller matematikvanskeligheder (Magne,1994).31Gudrun Malmer (2001) fremhæver, at den logiske tænkning børfå meget større betydning og plads. Dertil påpeger hun, at grundforud-sætningen for logisk tænkning er en kombination af matematisk ogsproglig kompetence. Derfor skal elevens erfaringer aktualiseres i forbin-delse med matematikundervisningen. Malmer mener, at der i højere gradskal afsættes tid til mundtlig matematik og handlingsmatematik. Det børprioriteres, at eleverne skal sætte ord på det, de ser og gør, da eleverneigennem italesættelsen tvinges til at tænke over, hvordan mekanismernefungerer.Blandt andre påpeger Engstrøm (2009), at begrebet dyskalkuli eruanvendeligt i det pædagogiske arbejde. For det første på baggrund afden store usikkerhed omkring definition, test, årsagsforklaringer og in-terventioner og for det andet, fordi begrebet knytter sig til en diagnosti-cering af eleven, hvilket Engstrøm ikke mener, hører hjemme i skolesy-stemet, men kun i lægeverdenen.I sin ph.d. afhandling problematiserer Sjöberg (2006, 2008) lige-ledes anvendelsen af begrebet dyskalkuli, når der er så mange tvivlsom-me og uklare omstændigheder omkring begrebet. Den empiriske del afSjöbergs undersøgelse viser endvidere, at feltet indeholder stor komplek-sitet. Denne empiriske del omfatter 200 børn, hvoraf 13 af dem har ma-tematikvanskeligheder. Resultaterne er baseret på indsamlede informati-oner om de 13 elever med matematikvanskeligheder. Eleverne angavblandt andet dårligt arbejdsmiljø, store klasser, stress og nervøsitet vedprøverne som forklaring på deres vanskeligheder i matematik. Derudover31. Se Magnes afsnit om neurologi.

har flere af eleverne i Sjöbergs undersøgelse negative opfattelser af lære-rene, og i de fleste tilfælde foretrækker de at henvende sig til medstude-rende. Undersøgelsen viste yderligere, at gode og dygtige lærere var medtil at nedbringe problemerne, såvel som at skoleskift og samarbejde medandre elever også havde positiv indvirkning på elevernes færdigheder.Uddannelseseksperten Jean Gross (2007) fremhæver, at man ibegyndelsen af implementeringsfasen til det britiske tiltag ”NationalNumeracy Strategy” (NNS), havde anvendt begrebet dyskalkuli defineretsom ”en tilstand, som påvirker evnen til at tilegne sig matematiske fær-digheder”. Senere udelod NNS dog begrebet grundet frygt for sygeliggø-relse af eleverne. Gross diskuterer i den forbindelse konsekvenserne veddiagnosticering. På den ene side kan diagnosticering medføre en risikofor over-investering af tid og energi, fordi diagnosen ikke formår atrumme alle børn med matematikvanskeligheder. Samtidig kan diagnoserog mærkater have negativ effekt på børns selvopfattelse, deres målrettet-hed og motivation for faget. På den anden side kan nogle børn opleve enlettelse ved diagnosticering, idet de herved får en forklaring på, hvorfornogle ting er særligt svært for dem, og at de ikke er ubegavede eller dov-ne.Uddannelsespsykolog James Gillum (2012) fremhæver ligeledes,at uddannelsespsykologer ikke er begejstrede for at anvende mærkater ogdiagnoser, men i stedet tager udgangspunkt i den enkeltes styrker ogsvagheder, læringsmiljøet samt løsninger på den enkeltes vanskeligheder.At sætte et mærkat på eleverne må derfor være sekundært. Han sætter iførste omgang også spørgsmålstegn ved mulighederne for, at uddannel-sespsykologer kan identificere dyskalkuli, hvor han henviser til denmanglende konsensus omkring en eksakt definition. Dog mener Gillumikke, at uddannelsespsykologer kan se bort fra dyskalkuli og særligt ikkefra den viden, som er fremkommet gennem neurobiologisk forskning.Gillum fremhæver, at neuroforskningen har identificeret struktu-rer i hjernen, som styrer individets evne til at forstå og bearbejde tal. Hanfremhæver endvidere, at forskningen ikke har påvist, at der er tale om enmedfødt mangel på talfornemmelse eller et afgrænset specifikt område afhjernen. Han pointerer, at forskningen viser, at der er tale om en kom-pleks proces, som involverer mange strukturer, og som udvikles som etresultat af interaktion mellem individet og dets miljø, herunder undervis-ningsmiljøet, snarere end at der er tale om en manglende talfornemmelseeller et afgrænset område af hjernen. Endvidere pointerer han dog, at

forskningen har vist, at nervesystemet pålægger nogle begrænsninger iforhold til en udvikling af talforståelse. Ifølge Gillum er der nemlig nogleområder af hjernen, som er forudbestemt for talbearbejdning og i de til-fælde, hvor disse områder er svækket, vil udviklingen af talforståelsentage en atypisk drejning (Gillum, 2012).Lunde (2006, 2000) giver også udtryk for et behov for et størrefokus på målrettede indsatser for ”matematikmestring” for elever medsærlige behov i matematik. På den måde får vi et positivt fokus på detspecialpædagogiske arbejde, snarere end at vi lægger vægten på diagnosti-ske mærkater. Lunde (2006) tager endvidere afstand fra ideen om, at ele-vers matematikfærdigheder eller -vanskeligheder er statiske. En del afårsagen til matematikvanskeligheder må ligge i undervisningsformen ogsamspillet mellem elev og lærer. I den sammenhæng fremhæver Lundeen finsk undersøgelse af Häggblom, som viser, at kun 20 pct. af elevernetilhører den samme præstationsgruppe gennem hele skoletiden. Argu-mentet er dermed, at langt de fleste elever flytter sig fagligt i takt med,deres udvikling og eventuelt i takt med, at de lærer nye strategier (Lunde,2006). Dette kan endvidere igangsætte tvivlspørgsmål om, hvorvidt dy-skalkuli er arveligt eller medfødt.Snorre (2006) omtaler tre forskellige definitionstilgange: diskre-pansdefinition, prokuradefinition og kendetegnsdefinition. Snorre an-vender dog begrebet ”dysmatematik” inspireret af Magne. Dysmatematikdækker både matematikvanskeligheder og dyskalkuli.Ved diskrepans er der tale om en markant uoverensstemmelsemellem børnenes dårlige matematikpræstationer og deres gennemsnitligeeller gode præstationer i andre fag, samt at deres matematikpræstationerligger under det forventet ud fra IQ-test og i forhold til barnets klassetrin.Prokura definitioner afgrænser sig til matematikrelaterede van-skeligheder efter et fastsat matematisk færdighedsniveau i forhold til,hvornår en matematikpræstation er god eller dårlig. Problemet med pro-kuradefinitioner er, at der er en høj risiko for at medregne elever, somikke har dyskalkuli og omvendt også en risiko for, at elever med dyskal-kuli ikke bliver medregnet.Kendetegnsdefinitioner er baseret på forskellige karakteristika,som kan sættes i sammenhæng med fænomenet, såsom vanskelighedermed verbalinternalisering (sproglyde) og primitive strategier. Snorre på-peger, at der er tale om et komplekst problem, der opstår i sammenhængmellem elevens indlæringsforudsætninger, matematikkens indhold og

Der er altså flere teorier om dyskalkuli. De mange faglige tilgange til dy-skalkuli kan være en styrke, der bidrager med forskellige vinkler på fæ-nomenet. De mange faglige tilgange og perspektiver skaber imidlertidogså problemer. Hvis der skal drages nytte af de forskellige perspektiverog tilgange, forudsætter det, at faggrupperne accepterer hinandens tilgan-ge som relevante, og ikke blot ser dem som en mangel. Det er nemligikke altid tilfældet. Det forudsætter også enighed om at skelne mellemdyskalkuli og generelle matematikvanskeligheder. De fleste af de sociolo-giske, psykologiske og didaktiske perspektiver vi har set på, handler omen bredere forståelse (generelle matematikvanskeligheder) snarere endom den specifikke vanskelighed, som vi her betegner dyskalkuli.De forskellige begreber og anvendelsesformer kan dog også væ-re udtryk for, at der findes helt forskellige typer problemer med at lærematematik. En del elever i folkeskolen får ikke lært den lille tabel, ogmange har svært ved at forstå og læse en matematisk problemstilling. Forenkelte hænger det sammen med, at de har svært ved at overskue småantal og mængder og ved at se, hvad klokken er på et analogt ur. For an-dre hænger det sammen med, at de ikke kan se fordelen ved eller menin-gen med at regne, eller at de har en emotionel blokering i forhold til faget.Som vi ser det, peger forskningen og viden tilsammen på, at vi ikke skaldebattere dyskalkulikontramatematikvanskeligheder, men i stedet erken-de, at der både findes specifikke vanskeligheder (dyskalkuli) hos et megetlille antal personer, og at der findes andre former for matematikvanske-ligheder hos et betydeligt større antal personer. I det næste afsnit skal vikort se på de subtyper, der fremhæves i litteraturen.

el/spatial dyskalkuli og numerisk-fakta dyskalkuli (Rosseli m.fl., 2006;Wilson & Deheane, 2007; Lunde, 2008b).32Semantisk dyskalkuli omhandler sproglige problemer i matema-tik, fx at huske hvad tallene hedder, hvad ordet ”division” betyder, ogden enkelte kan dermed have vanskeligheder ved at arbejde med tekst-problemer, herunder læse- og skrivevanskeligheder, begrebsvanskelighe-der, hukommelsesproblemer, langsom bearbejdning mv.Procedure dyskalkuli drejer sig om vanskeligheder med række-følge, strategi, orden og fremgangsmåder. Den enkelte vil have svært vedat forstå og bruge regneregler.Visuel/spatial dyskalkuli knytter sig til det rumlige og visuelle,forståelsesproblemer med former, mønstre og ting i forhold til hinanden,fx vanskeligheder ved at læse viserne på et ur, læse visuelle illustrationer,at finde fra A til B, højre-venstre, nord-syd-øst-vest.Numerisk-fakta dyskalkuli drejer sig om den enkeltes forståelsefor tal og mængde, hvilket kan give eksplicitte problemer med plus, mi-nus, gange og division. Når denne basisforståelse har mangelsider kanrækkefølger og regler ikke følges.CSV påpeger ligeledes, at der findes flere former for dyskalkuliog flere sværhedsgrader. Nogle elever kan fx godt være gode til geometri,men samtidig have store vanskeligheder ved simple plus- og minusregne-stykker. Det fremhæves, at symptomer på dyskalkuli kan være, at elevenhar svært ved at læse tal, selvom han/hun kender de enkelte cifre, samtdårlig retningssans og tidsfornemmelse, svært ved at kende forskel påhøjre og venstre mv., men at den enkelte elev ikke nødvendigvis harproblemer med alle områderne på én gang (CSV, 2010; Grynberg, 2010).Dyskalkuli anses altså også som synonym eller samlebetegnelsefor en række andre forhold. Det vil sige, at dyskalkuli både anses for atvære en blandt flere årsager til matematikvanskeligheder generelt, mendet kan også ses som en samlet betegnelse for flere beslægtede fænome-ner.Samlet set er dyskalkuli altså ikke entydigt defineret. Langt defleste er imidlertid enige om, at problemet findes. Yderligere er der en visenighed om, at der mangler en konkret og alment accepteret definition afdyskalkuli. Overordnet set omfatter dyskalkuli specifikke problemer medtal, hvor personen ikke følger den normale faglige udvikling og desudenhar en gennemsnitlig IQ eller derover.32. Også Ostad og Reikerås omtaler disse elle lignende subtyper.

Inddrager vi alle fire perspektiver (neurologiske, psykologiske,sociale og didaktiske), som de er gennemgået her, kan vi sige, at vi bevæ-ger vi os over i en bredere forståelse, her forstået som matematikvanske-ligheder eller regnehuller, hvor dyskalkuli begrænser sig til de neurologi-ske aspekter. Samlet set er der altså tale om primære og sekundæreaspekter af dyskalkuli. Som vi ser det, dækker det neurologiske perspek-tiv de primære aspekter af dyskalkuli, hvor de psykologiske, sociologiskeog didaktiske perspektiver dækker sekundære aspekter af dyskalkuli.Sidstnævnte aspekter kan dog også forekomme uden, at der er tale omdyskalkuli.Ser vi på de primære aspekter, er der for det første bred enighedom, at årsagen på den ene eller anden måde kan kobles til funktioner ihjernen. For det andet er der enighed om, at dyskalkuli indebærer, at denenkelte har (specifikke) problemer med tal. For det tredje har vedkom-mende ikke vanskeligheder på andre områder, det vil sige, at vanske-lighederne er centreret omring tal og talbehandling. Ser vi på de sekun-dære aspekter, bevæger vi os over i bredere definitioner og betegnelser,såsom regnehuller eller matematikvanskeligheder. Her er der i vid ud-strækning enighed om, at det ikke er et fænomen, som isoleret set kanafgrænses til individet, men at der er tale om et sammensat problem(neurologisk, psykologisk, sociologisk og didaktisk). Dyskalkuli kan altsåvære en medvirkende faktor til matematikvanskeligheder, men den har isig selv ingen sammenhæng med øvrige vanskeligheder.Begrebet matematikvanskeligheder anser vi derfor for at dækkeover det forhold, at personer kan komme i vanskeligheder med tal ogmatematik på baggrund af flere samspillende faktorer (neurologiske, psy-kologiske, sociologiske og didaktiske). Dertil bliver vanskelighederneknyttet til de færdigheder, der bliver forventet i forbindelse med fagetmatematik.Dyskalkuli, som denne rapport omhandler, anser vi som enfunktionsnedsættelse, der er knyttet til den enkeltes (medfødte) evner tilat forstå tal og størrelser, hvilket ikke har en sammenhæng med vanske-ligheder i øvrigt.

Der er enighed om, at dyskalkuli ikke er entydigt defineret og en visenighed om, at de definitioner, der findes, ikke er dækkende ellerpraktisk anvendelige.Der er enighed om, at dyskalkuli kan kobles til funktioner i hjernen.Det skal dog understreges, at hjernen er plastisk og hele tiden udvik-ler sig.Der er generelt enighed om, at personer med dyskalkuli især harvanskeligheder med tal- og mængdeforståelse, herunder har sværtved at lære og huske aritmetiske fakta og at udføre simple regnepro-cedurer. Disse vanskeligheder fremgår på trods af gode eller gen-nemsnitlige evner i øvrigt.Dyskalkuli kan være en samlebetegnelse for andre forhold, såsomvanskeligheder ved matematiske procedurer, visuel/spatiale forholdog numeriske fakta.Dyskalkuli kan omfatte yderligere andre typer af vanskeligheder in-den for psykologiske, sociologiske og didaktiske områder, såsomangst eller en negativ holdning til faget matematik, som vi anser forat være sekundære vanskeligheder,

En del af formålet med denne kortlægning af anvendte definitioner er atfinde frem til en anvendelig definition på baggrund af konsensuspunk-terne.Først skal vi fremhæve, at vi har valgt at anvende betegnelsendyskalkuli, dels fordi det er en del af den officielle betegnelse (sammenmed specifikke regnevanskeligheder, jf. ICD-10). Dels fordi det er denbetegnelse, der anvendes internationalt, og dels fordi der er flere forskere,der peger på de negative associationer, der følger med ordet ”vanske-ligheder”. Derudover skelner vi mellem dyskalkuli, som vi ser som denprimære vanskelighed og andre typer af matematikvanskeligheder, som vii dette tilfælde anser for at være sekundære vanskeligheder.Vi er således nået frem til følgende forslag til en definition:Dyskalkuli er en funktionsnedsættelse, der kan have negativ ind-virkning på den berørtes uddannelses- og arbejdsliv. Tilstandendrejer sig om tilbagestående regnefærdigheder, som ikke mod-svares af tilsvarende tilbagestående færdigheder på andre felter.De specifikke regnevanskeligheder omfatter påfaldende vanske-ligheder med at forstå og håndtere basal talbehandling, såsom atsammenligne tal og antal i mængder eller tælle små antal gen-stande. I forlængelse heraf er der påfaldende vanskeligheder vedaddition, subtraktion, multiplikation og division. Tilstanden om-fatter ikke nødvendigvis vanskeligheder med mere abstrakte ma-tematiske færdigheder i algebra, trigonometri, geometri og kom-plekse beregninger. Vi taler ikke om dyskalkuli, hvis baggrundenfor vanskelighederne er mental retardering eller mangelfuld sko-legang. Dog kan tilstanden omfatte kognitive problemer sommangelfuld semantisk hukommelse og arbejdshukommelse.I tilknytning til definitionen kan vi sige, at hvis der er tale om konsekven-ser af kognitive eller emotionelle problemer, falder det ikke ind underdefinitionen på dyskalkuli, men dyskalkuli kan føre til sekundære vanske-ligheder som angst og dårligt selvværd. Dyskalkulikere vil ofte udvisegode eller middel præstationer ved abstrakte matematiske færdigheder,men kan samtidig have vanskeligheder med ting som at aflæse et analogtur, finde et husnummer eller forstå en togplan.Tilstanden omfatter altså ikke vanskeligheder ved den mere avancere-de ”skole-matematik”. I litteraturen fremgår det, at dyskalkulikere kan

være dygtige til mere avancerede og abstrakte matematiske opgaver, i fxalgebra, trigonometri, geometri og komplekse beregninger, hvilket ogsåbekræftes af flere eksperter. Dyskalkulikere vil derimod have påfaldendevanskeligheder med helt basal tal- og mængdehåndtering. Det betyder, atdyskalkulikere ikke nødvendigvis kan identificeres på baggrund af stan-dardiserede matematikprøver.I det næste kapitel skal vi se nærmere på test, der kan være medtil at identificere tilstanden og dermed handlemuligheder. Først vil vi dogkort præsentere et estimat for, hvor mange mennesker tilstanden drejersig om.

Eksperter vurderer, at 1-6 pct. af befolkningen har dyskaluli i en elleranden grad. Estimatet varierer afhængigt af, hvordan dyskalkuli defineres.Magne (2004) taler som nævnt om SUM-elever. En SUM-elevdefineres ved, at hun/han ikke har opnået de uddannelsesmål, som erblevet angivet i læreplanen. Magne påpeger, at ca. 10-15 pct. i den sven-ske befolkning har matematikvanskeligheder (Magne, 2004). Dog dækkerMagnes estimat over en bredere definition (jf. ovenstående afsnit omdefinitioner og begreber).I 1994 fandt Lewis, Hitch & Walker frem til, at 1,3 pct. af ver-dens befolkning har dyskalkuli, mens 2,3 pct. både har dyskalkuli og dys-leksi. Gros-Tsur, Manor & Shalev fandt i 1996 frem til, at 6,5 pct. af ver-dens befolkning har dyskalkuli. Ifølge Butterworth m.fl. (2011) har mel-lem 5-7 pct. af befolkningen dyskalkuli, hvilket svarer nogenlunde tilsamme procentdel, der lider af dysleksi (ordblindhed).Ifølge Kaufmann & Aster (2012) drejer det sig om ca. 5 pct. fol-keskolebørn. De fremhæver, at de 5 pct. er et relativt stabilt estimat, derforekommer på tværs af de lande, der bedriver forskning om emnet.Kaufmann og Aster anvender WHO’s definition, som vi har beskrevet istarten af dette kapitel.Netop på grund af den manglende konsensus omkring begrebetmå vi endvidere antage, at der også må være en andel, der aldrig bliverudredt for dyskalkuli. Samtidig må vi også antage, at personer, der ikkehar dyskalkuli, men måske andre vanskeligheder relateret til matematik,bliver medregnet.

TESTI dette kapitel vil vi kortlægge det eksisterende testmateriale, som vi harfundet frem til. De test, vi fremlægger her, har vi lokaliseret i forbindelsemed vores litteratursøgning og med hjælp fra danske eksperter på områ-det. Vi skal her pointere, at langt de fleste af de test, vi har fundet frem til,har vi ikke haft direkte adgang til. Dette afspejler sig blandt andet i test-beskrivelserne, hvoraf nogle beskrivelser er mere omfattende end andrepå baggrund af, hvor mange informationer der har været tilgængelige.Kapitlet vil så vidt muligt omfatte beskrivelser af, hvordan eksisterendetestmateriale bliver anvendt, herunder hvilke målgrupper testene hen-vender sig til, hvornår der bliver testet, og hvilke færdigheder der bliverafdækket. Afslutningsvis vil vi opsummere de områder, hvor vi finder envis konsensus i forhold til, hvad der er relevant at teste.Som vi så i forrige kapitel, er der blandt forskere og praktikeregenerelt enighed om, at dyskalkuli og matematikvanskeligheder ikke erdet samme. Det hersker snarere en diskussion om, hvorvidt begrebetdyskalkuli er brugbart i praksis, særligt når der ikke er enighed om, hvaddet indebærer. Som det fremgår af vores kortlægning af definitioner, fin-des der en stor gruppe eksperter, som ikke finder en dyskalkuli-diagnoseanvendelig i det praktiske arbejde. De fleste personer med fokus på sko-len og læreprocesser frygter de negative konsekvenser, ved at sætte mær-kater på eleverne. Denne gruppe eksperter har en meget vigtig pointe.

Det giver nemlig kun mening at diagnosticere, hvis det gør det muligt athandle på diagnosen. Derfor giver diagnosen dyskalkuli kun mening, hvisden betyder, at fx skolen kan igangsætte en indsats, ved at eleven får etrelevant og fyldestgørende undervisningstilbud. Foreløbige erfaringer fraet nyligt opstartet projekt i Region Nordjylland viser en positiv effekt afdiagnosticering, hvor diagnosen og den tilhørende hjælp har øget elever-nes selvværd og været med til at forebygge frafald på grund af regnevan-skeligheder. Dette projekt beskriver vi nærmere under test-beskrivelserne.For elever med dyskalkuli vil det også være relevant, at indsatsener bredt forankret og dermed også håndterer de sekundære aspekter,herunder psykologiske, sociologiske og didaktiske. Det kan fx dreje sigom emotionelle blokeringer eller matematikangst, der er opstået pågrund af dyskalkuli, således at eleven (igen) får et positivt forhold til ma-tematik. Fra Undervisningsministeriets side er det ligeledes centralt, atdyskalkuli-testen vil fokusere på handlemuligheder i stedet for forklarin-ger.I de følgende afsnit vil vi belyse konsensuspunkter i litteraturenvedrørende test inden for dyskalkuli-området. Dernæst vil vi beskriveeksisterende testmateriale, som skal underbygge konsensuspunkterne.Som indledning til testbeskrivelserne behandler vi kort debatten omkringbrug af test, som den fremgår i litteraturen. Sidst i rapporten findes enskematisk oversigt, hvor fokus især er på de test, vi beskriver her.

Samlet set er der konsensus om, at det for det første er vigtigt atvide noget om, hvad eleven kan og ikke kan, herunder om eleven harandre vanskeligheder. For det andet er det gennemgående i litteraturen,at det er vigtigt at vide noget om processerne bag elevens svage og stær-ke sider samt at få viden om, hvordan eleven lærer. For det tredje er detvigtigt at vide noget om elevens sociale trivsel i skolen, derhjemme og ifritiden. Dertil er der også vægt på skolens didaktiske kompetencer, oghvad der findes af lærekompetencer og materialer.Vi ser derfor også en vis konsensus i litteraturen om, at eleverneskal testes bredt. I vores gennemgang af test er det gennemgående, ateleverne bliver screenet eller testet i meget forskellige færdigheder medvægt på både neurologiske, psykologiske, sociologiske og didaktiskeaspekter. I forhold til hvad der skal testes, kan konsensuspunkterne i lit-teraturen opdeles i to niveauer: et overordnet niveau og et specifikt ni-veau:OVERORDNET

Kognitiv udvikling, funktioner og evner, hvilket giver et billede afelevens forudsætninger, herunderverbalforståelse, perceptuel ræsonnering,arbejdshukommelse og forabejdningshastighed.Matematiske præstationer og grundlæggende færdigheder i forholdtil de konkrete discipliner inden for det faglige område med ud-gangspunkt i elevens forventede niveau (i forhold til alder, klassetrinmv.). Dette giver et billede af elevens matematiske standpunkt, her-undertalforståelse, addition, subtraktion, multiplikation, division, problemløs-ning, hukommelse, koncentration opmærksomhed, før-faglige begreber, rum-retning (spatial) og form og størrelse.Trivsel og omgivelser, herunderangst, motivation, koncentration, holdningtil faget samt forhold til forældre, lærer, klassekammerater og andre relationer.

Overordnet set bliver elever med dyskalkuli beskrevet som elever, derkontinuerligt underpræsterer i standardiserede test og elever, der oplevergenerelle problemer med at opfylde forventede mål. Ved kun at anvendestandardiserede matematiktest, eventuelt suppleret med en intelligenstest,er der en stor risiko for, at mange elever, som ikke har dyskalkuli, endermed at få diagnosen. Omvendt er der en risiko for at børn med dyskal-kuli bliver overset. Personer med dyskalkuli kan nemlig klare sig rigtiggodt i forhold til nogle matematiske områder og dårligt i forhold til andrematematiske områder. Samtidig giver en standardiseret test ikke indblik ikarakteristiske strategier, såsom fingertælling.SPECIFIKT

Dertil kan ovenstående punkter forårsage angst eller negative holdningertil matematik.Enkelte eksperter fremhæver, at hvis neurologerne har ret, vil vivære ud over, hvad eleven har lært, eller hvem der har undervist, ellerhvad forældrene tænker om matematik (psykologiske, sociologiske ogdidaktiske aspekter). Dertil skal lægges behovet for en samtale, somtrænger ned i egentlige faglige og kognitive vanskeligheder, holdnings-mæssige psykologiske faktorer samt omgivelsernes påvirkning. Dennesamtale skal pege mod nogle ændrede pædagogiske praksisser og andetindhold.

En centralt stillet test – papir eller elektronisk skal så vidt mulig væreakulturel og uddannelsesuafhængig. Vi skelner her til neurologerneButterworth og Deheane, som mener at kunne påvise, at der er enstartudrustning knyttet til skøn af mængder og små antal, som ermere skrøbelig hos nogle mennesker end andre – og at der kan lavesen følgeslutning om, at en sådan skrøbelighed har følgevanskelighe-der inden for håndtering af numeriske størrelser med de tegn, somalmindeligvis nævnes (pengehåndtering, det analoge ur osv.). En så-dan test giver IKKE anvisning på undervisning, men kan måskesynliggøre mulige specifikke vanskeligheder. Brian Butterworthsdyscaculia screener er et udtryk for dette. Bjørn Adler har fabrikereten test, hvor man skal overskue mængder, men som vi ikke kenderkvaliteten på.De personer, som via en sådan central stillet test synes at have ensådan skrøbelig udrustning, kunne betegnes som en mulig risiko-gruppe. De skal først gennem en samtale med en faglig kvalificeretsamtalepartner ud fra en samtaletest, som undersøger såvel primærefaglige vanskeligheder, men også sekundære kognitive vanskelighe-der, kortlægger mulige psykologiske faktorer samt holdningsmæssigeforhold knyttet til undervisning og dernæst laves en profil af kon-flikter mellem fag, individ og omgivelser.De to første punkter skal have en pejling mod, at undervisningenbliver forbedret34, ellers giver de første to punkter ikke mening. For-eningen tror dog ikke, at der er lavet tilstrækkelig meget forsøg medat tænke undervisning for disse elever, der kan være i risikogruppenpå en anden måde. Der er forskere, som mener, at det bare er ”al-mindelig god undervisning”, men DanSMa tror, at der er dele af enundervisningsdifferentiering, som har særlige vægtninger for disseelever frem for andre. Det drejer sig om at bruge hjælpemidler på enanden og mere systematisk måde på baggrund af en forståelse af, atdisse ”risikoelever” typisk kan forstå mere abstrakt matematik osv.

Der bør testes bredt for at udelukke andre vanskeligheder og samti-dig vurdere sekundære vanskeligheder, samt om vanskelighederne ersekundære eller primære. Elevens omgivelser skal også inddrages forat få et helhedsbillede af barnets situation.Tænkning og strategier bør gøres eksplicitte via observation og sam-tale i forbindelse med hverdagsaktiviteter og leg, hvor matematikkensystematisk integreres, og barnet italesætter sine handlinger.Børnene kan screenes i grupper eller klasser, men en egentlig vurde-ring af det enkelte barn må foregå individuelt, hvor der er mulighedfor dialog omkring barnets strategier, oplevelser og følelser.

Stort set alle de eksperter, vi løbende har været i kontakt med, er enigeom, at det er meget risikabelt at diagnosticere eleverne for tidligt. Defremhæver, at de første skoleår kan påvirke eleverne meget forskelligt.Samtidig udvikler eleverne sig meget forskelligt og i forskellige tempi.Flere af eksperterne anbefaler derfor, at eleverne i løbet af de første sko-leår kan screenes og observeres. Som det fremgår af testbeskrivelsernesenere i dette kapitel, kan børn allerede observeres og screenes fra to-årsalderen. I litteraturen er der ligeledes gennemgående konsensus om, atbørn ikke udvikler sig lineært, og at der samtidig kan være mange forskel-lige årsager til, at børnene kan have svært ved tal og regning. Flere ek-sperter fremhæver, at disse årsager især kan være svære at identificere i detidlige år. På den baggrund er der enkelte eksperter samt foreningenDanSMa, der udtaler, at det først giver mening at teste og diagnosticerebørnene for dyskalkuli omkring 4. klassetrin, hvor de er mere etableredeog har vænnet sig til at gå i skole. I litteraturen er vi ikke stødt på decide-rede test til før-skolebørn, dog er vi stødt på observationsmaterialer ret-tet mod børn fra omkring to-årsalderen, hvilket fremgår af testbeskrivel-serne senere i dette kapitel.

Eksperter fra DanSMa er af den opfattelse, at der er mulighederfor at beskrive opmærksomhedstegn hos elever med særlige vanskelighe-der, herunder tegn på specifikke vanskeligheder knyttet til et talblind-hedsfænomen. Deres oplevelse og erfaring – både egne erfaringer og frasamtaler med lærere og specialpædagoger samt kendskab til forskning ogdrøftelse med forskere – er, at der kan være for mange faktorer, fx kor-morbiditetsproblemer, der slører billedet for meget, hvis man er for tid-ligt ude. De påpeger derfor, at det ikke er rimeligt at diagnosticere førmellemtrinet, så forskellene kan være tilstrækkelige tydelige. Med sammevidensbaggrund påpeger eksperter fra DanSMa, at tidlig kortvarig kon-centreret indsats ikke synes at have tilstrækkelig stor effekt på de elever,som er målgruppen i denne rapport. De pointer dog, at de mener, at derkan komme meget positivt ud af det – ikke mindst på det motiverendeplan – men at der ikke sigtes bredt nok set i forhold til de elever, somikke har helt så massive vanskeligheder.35Det er således foreningensholdning, at her skal der tænkes i en langstrakt indsats gennem formo-dentlig hele skoleforløbet, hvor man skal planlægge undervisning oghjælpeforanstaltninger, og hvor eleverne lærer at håndtere en funktions-nedsættelse, som flere af dem vil have resten af deres liv.I det følgende afsnit vil vi beskrive de forskellige test, vi er stødtpå i vores litteratursøgning, og som vi har fået anbefalet af eksperter.

De seneste år har der været meget fokus på standardiserede og nationaletest. Målsætninger og styringsinstrumenter i forvaltningen er blevet højtprioriteret, og testene skal fungere som et værktøj til at sikre en fagligstandard og udvikling ved at kontrollere, om eleverne lærer det, som deskal.Debatten om testning og betydningen for eleverne er især blus-set op efter 2010, hvor de nationale test blev gjort obligatoriske i landetsfolkeskoler – også for lavt præsterende elever og elever i specialskoleregi.Inden for test- og evalueringsteori taler man om både negative og positi-35. DanSMa fremhæver i den forbindelse et forsøg, der er udført i Sorø omkring tidlig indsats (dogmed få elever). Dertil fremhæver de, at Brian Butterworth problematiserer dette i sin bogDyscal-culia,samt at problematikken omtales af folkene bag TIM. De fremhæver endvidere EMU-projektet i Australien, der også omtaler en ”hard core”- gruppe på omkring 4-5 pct., hvor indsat-sen ikke har tilstrækkelig effekt.

vewash-back-effekter.En negativ wash-back-effekt kan eksempelvis væresåkaldt ”testlæring”: at underviserne afgrænser deres undervisning til det,eleverne bliver testet i. Omvendt kan en positivwash-back-effektvære, ateleverne i højere grad repeterer. Det kan dog samtidig føre til, at elevernebliver særligt testkompetente, men ikke har fuld forståelse for det lærte(The Agency, 2013; Nordenbo m.fl., 2009). Yderligere er der risiko for,at sociale forskelle bliver forstærket, hvilket kan resultere i reduceret læ-ring, manglende motivation og lavt selvværd hos de elever, der scorerlavt i testene (The Agency, 2013; Sjöberg & Nuroos, 2009; Sjöberg, 2006;Kousholt, 2009). Testning kan på den måde også have en ekskluderendeeffekt og stille svage elever endnu svagere.Imidlertid kan testning også bidrage med viden om elevernesfærdighedsniveau og eventuelle vanskeligheder, således at der kan sættesind overfor disse vanskeligheder, og hvormed der bidrages til en positivwash-back-effekt (The Agency, 2013).Hvis en test skal kunne anvendes i praksis og samtidig sikre enrelevant indsats for den enkelte elev med dyskalkuli, er det for det førsteafgørende, at der er et fælles udgangspunkt og konsensus om definitio-nen af dyskalkuli. En dyskalkuli-test bør bidrage med viden om, hvordanpersoner med dyskalkuli adskiller sig fra andre, fx personer med matema-tikvanskeligheder. I forlængelse heraf skal en dyskalkuli-test give et ind-blik i, hvad der skal til, for at personer med dyskalkuli kan lære at be-handle tal. Når skolerne skal udrede eleverne for dyskalkuli, må testenaltså som udgangspunkt være baseret på den samme definition og der-med de samme kriterier. Definitionen er altså helt afgørende i forbindel-se med at udvikle en relevant test, da det er de kriterier, der opstilles idefinitionen, som en given test må tage udgangspunkt i.I de følgende afsnit skal vi se nærmere på, hvilke test der domi-nerer i litteraturen, og hvilke kriterier de tager udgangspunkt i og dermedundersøger. Udover test med specifikt fokus på dyskalkuli, har vi ogsåinddraget øvrige test, der bliver fremhævet i litteraturen samt af eksperter.Dette inkluderer test, som har fokus på matematikvanskeligheder ellerkognition. Vi har valgt at inddrage de øvrige test, dels fordi det er de fær-reste test, der specifikt undersøger dyskalkuli, og dels fordi litteraturenanbefaler, at de forskellige test inden for hver deres område ikke står ale-ne.

Brian Butterworth (2003) har selv udviklet en dyskalkuli screener, som eren computerbaseret screeningstest. Den henvender sig til børn i alderen6-14 år. Butterworth tager udgangspunkt i, at dyskalkuli er en medfødtfunktionsnedsættelse. Dette bygger han på neurologisk forskning, derindikerer, at mennesket har en medfødt evne til at skønne antal ellermængder.36Screeningstesten afdækker derfor først og fremmest elevens in-tuitive mængdeforståelse og talfornemmelse. I testen bliver elevens be-svarelser målt på reaktionstid og antal rigtige svar. I testen bliver der fxvist et tilfældigt antal emner (fx prikker, stjerner eller andet) på skærmen,og personen skal angive, hvor mange emner der er. Skærmen kan ogsåvise to kasser samtidig med et tilfældigt antal emner i hver. Her skal per-sonen angive, hvilken kasse der indeholder flest prikker (se figur 4.1).For begge typer har testpersonen et begrænset tidsrum til besvarelsen ogskal reagere så hurtigt som muligt.

der er mere end fire prikker, og når de samtidig ved, at de tester på tid.Dyskalkulikere vil oftest være tvunget til at tælle prikkerne enkeltvis –også når der er mindre end fire genstande. Testene i figurerne figur 4.1og figur 4.2 kan bidrage med informationer om, hvorvidt personens van-skeligheder er grundet i dyskalkuli eller andre kognitive vanskeligheder.Med hensyn til hvilket tal der fysisk er størst, besvarer dyskalkulikere ligeså hurtigt og præcist som personer uden vanskeligheder. I forhold tilhvilket tal der har den største talmæssige værdi, er dyskalkulikere længereom at svare og svarer ofte forkert. Jo tættere talværdierne er på hinanden,des mere kompliceret bliver opgaven. Resultaterne bliver sammenlignet –også med andre målinger, som Butterworth mener, er associeret medtilstanden dyskalkuli37. Overordnet omtaler Butterworth færdigheder iforhold til områderne: numerisk fakta, taloperationer og positionssyste-met.Gillum (2012) har kritiseret Butterworths dyskalkuli-screener påbaggrund af, at computerprogrammet vurderer børnenes regnefærdighe-der og talfornemmelse gennem måling af deres svartid. Gillum påpegerher, at nogle børn mister koncentration og entusiasme efter det førstestykke tid, mens andre er nervøse ved test. Begge dele er parametre, derkan spille ind på børnenes svartid og dermed på resultaterne.JAN EMERSON OG PATRICIA BABTIE: THE DYSCALCULIA ASSESSMENT(DYSKALKULI-VURDERINGEN)

Emerson & Babties dyskalkuli-vurdering (Dyscalculia Assessment) ersærlig anvendelig, hvis der er markant diskrepans mellem barnets gene-relle intellektuelle niveau og dets regnefærdigheder. Diskrepansen bliverblandt andet afgjort ved at sammenligne barnets matematiske færdighe-der med andre færdigheder, såsom verbale evner og læsefærdigheder.Ved hjælp af dyskalkuli-vurderingen kan testtageren efterfølgende ind-kredse, hvilke specifikke regnevanskeligheder barnet har. Emerson &Babtie understreger, at vurderingen ikke kan bruges til at diagnosticereen tilstand.Ifølge Emerson & Babtie er det helt essentielt at finde frem tildet punkt, hvor barnet ikke er i stand til at erhverve faktuelle eller meto-diske aspekter, som er afgørende for udviklingen af talforståelse. Vedhjælp af vurderingen skal testtageren undersøge barnets viden og evner.Dertil bliver barnets omgivelser inddraget for at skabe et helt billede afelevens vanskeligheder. Under vurderingen bør der anvendes en multi-sensorisk tilgang, hvor fx objekter bliver inddraget for sammen med bar-net at undersøge matematiske ideer og strategier, som italesættes.Emerson & Babtie fremhæver, at det er nødvendigt både at ska-be overblik over, hvad eleven kan og ikke kan, men også over, hvordanden enkelte elev tænker i forhold til matematik, herunder elevens strate-gier for opgaveløsning. Ved at undersøge hvordan den enkelte elev tællerog udfører simple regnestykker, er det muligt at nå frem til, hvilke kon-krete vanskeligheder den enkelte har. Samtidig giver det mulighed for atvurdere, hvilket matematisk udviklingsniveau barnet er på. Yderligeregiver det mulighed for at vurdere, hvordan barnets vanskeligheder kanblive afhjulpet i forhold til at opbygge barnets forståelse for tal og reg-ning. Vurderingen giver endvidere indblik i generelle aspekter, der kanindikerer, hvordan barnet har det med læring både generelt og specifikt iforhold til matematik, herunder barnets selvtillids- og angstniveau.Resultaterne er ikke standardiserede, da de kun relaterer sig tildet barn, der bliver vurderet. Ved hjælp af den opsummerende matema-tikprofil kan fx læreren sammenligne resultater børnene imellem, hvisformålet er at gruppere børnene i forbindelse med undervisning. Emer-son & Babtie deler vurderingsprocessen i tre faser:1. Introducerende samtale med barnet; Testtageren taler med elevenom, hvad eleven kan lide og ikke kan lide ved at gå i skole, hvad ele-ven generelt er glad for, hvordan eleven har det med matematik,

hvilke aspekter eleven oplever at kunne gennemføre, og hvilke ele-ven ikke mener at kunne gennemføre, samt hvilke aspekter der ersærligt svære osv.2. Dyskalkuli-vurderingen – en struktureret undersøgelse. Vurderingener ikke tidsafgrænset. Den søger via strukturerede formuleringer atopmuntre eleven til at fortælle, hvad hun/han gør, og hvad hun/hantænker om det. Testtageren kan modificere formuleringerne, mendet er afgørende, at eleven forstår meningen, og at alle spørgsmål erkorte. Undervejs er det vigtigt, at barnet bliver rost og opmuntret, ogat der så vidt muligt bliver skabt tryghed og god stemning. Testtage-ren skal ikke fortælle barnet, om hun/han gør det rigtigt eller forkert.Testtageren skal primært lytte til barnets ræsonnementer og observe-re barnets reaktioner. I vurderingen skal barnet udføre forskelligeøvelser, der starter på et basalt regneniveau og arbejder sig op modmere avancerede opgaver. Hvis barnet har 2-3 fejl i en sektion, gårtesteren videre til næste sektion. På samme måde hvis barnet klarerde basale regnestykker uden vanskeligheder og med relevante ræ-sonnementer, går testtageren videre til mere avancerede opgaver ef-ter 2-3 øvelser. Erfaring viser, at børn med talproblemer ofte harproblemer med basal eller simpel talforståelse og fornemmelse formængder. De første sektioner, hvor fejl bliver opdaget, vil forment-lig indikere, hvor der skal sættes ind.3. Information bliver indhentet fra andre kilder. Forældre, lærere ogandre professionelle bliver inddraget for blandt andet at udelukkeandre vanskeligheder, der kan spille en rolle i forbindelse med bar-nets regnevanskeligheder.a. I forhold til diagnosticering anbefaler Emerson & BabtieBa-sic Number Screening Testfra Gilham & Hesse39, som lærere kanudføre. Desuden anbefaler de, at skolepsykologer eller klini-ske psykologer bliver inddraget, da de kan vurdere barnets in-tellektuelle evner og funktioner, fx via WISC.b. Fysioterapeuter og ergoterapeuter kan blive inddraget for atvurdere barnets motoriske udvikling, hvilket kan have indfly-delse på barnets generelle udvikling.c. Talepædagoger kan inddrages for at undersøge barnets tale-færdighed og måden, barnet anvender sprog på (fx hvordanbarnet forstår ord og udtrykker sig).39. Gilham & Hesses test er standardiseret og tager udgangspunkt i nationale mål.

Selve dyskalkuli-vurderingen (punkt 2) tager ca. 1 time eller mindre. Dogbehøver man ikke at gennemføre hele vurderingen på én gang, men kandele den op i flere sessioner. Vurderingen er opdelt i seks sektioner 1)talsans og tælling (number sense and counting), 2) regning (calculation), 3)positionssystemet (place value), 4) multiplikation og division (multiplica-tion and division), 5) problemløsning (word problems) og 6) formelskriftlig talforståelse (formal written numeracy). Den første sektion be-står af basale opgaver, og de efterfølgende sektioner bliver mere avance-rede.COLIN MCCARTHY, KEN HESSE & BILL GILHAM: BASIC NUMBERSCREENING TEST

Emerson og Babtie (2010) anbefaler denne test til diagnosticering. Te-sten er ifølge forfatterne en hurtig og pålidelig vurdering af børns talfor-ståelse og -operationer. Formålet er at finde frem til de børn, som harbehov for støtte. Testen er baseret på den nationale undervisningsplan(Storbritannien) for 1.-5. klassetrin, hvilket også er målgruppen for testen(ca. 5-12 år). Testen leveres mundtligt, så den kan fokusere på elevernesregnefærdigheder snarere end på deres læsefærdigheder. Ifølge forfatter-ne er den derfor ideel til børn med læsevanskeligheder samt de yngstebørn. Testen er udformet, så den let og hurtigt kan udføres samt revur-deres senere for at vurdere elevens fremskridt. Testen kan udføres klas-sevis eller individuelt.STEVE CHINN: DEALING WITH DYSCALCULIA-ASSESMENT/DIAGNOSIS

Chinn tilbyder selv en vurdering og diagnose for matematikvanskelighe-der og dyskalkuli via test og procedurer. Til formålet har han blandt an-det også udgivet bogen (2012)More Trouble with Maths: A Complete Guide toIdentifying and Diagnosing Mathematical Difficulties,hvor hans test og proce-durer er inkluderet. Processen er skræddersyet til det enkelte barn og kanomfatte en test af nuværende præstationsniveau, angstspørgeskema, testfor viden om basale fakta, en udforskning af barnets tænkning og strate-gier i forhold til matematik samt uformelle kliniske aktiviteter.Chinn (2009) påpeger, at mennesker kan være stærke og svageinden for specifikke områder, hvilket også gælder inden for matematik.Ifølge Chinn er det muligt at vurdere, om et barn har dyskalkuli. Hvisbarnet præsterer under det forventede, og det ikke skyldes andre fysiskeeller psykiske funktionsnedsættelser, er der, ifølge Chinn, tale om dyskal-

kuli. Han har udviklet en liste med 31 spørgsmål, som kan hjælpe en per-son med at finde ud af, hvilke problemer personen har inden for mate-matik. Hvis den pågældende person har vanskeligheder i forhold til halv-delen eller flere af spørgsmålene, har personen sandsynligvis dyskalkuli.Chinn har desuden en matematikangst-test, som er frit tilgænge-lig på hans hjemmeside.40Testen kan hjælpe den enkelte til at forstå,hvordan denne har det i situationer, hvor matematik indgår. Testen be-står af 20 forskellige spørgsmål om konkrete situationer, hvor personenpå en skala fra 1-4 skal vurdere, hvor angst denne bliver i de opremsedesituationer. Svarmulighederne fra 1-4 omfatter; 1) aldrig angst, 2) angst afog til, 3) ofte angst og 4) altid angst. Spørgsmålene kan fx handle om,hvordan man har det i forskellige situationer, når man handler med pen-ge, følger en opskrift, læser en togplan, udarbejder et hjemmebudget mv.Hvis personen får en samlet score på 60 eller derover, vil det betyde, atpersonen generelt er meget angst i situationer, hvor matematik indgår.En score på 34 er normalen (Chinn, 2007).De test der har særlig fokus på dyskalkuli lægger først og frem-mest vægt på den intuitive talfornemmelse, herunder forståelsen for talog antal, men også andre aspekter bliver undersøgt. De forskellige aspek-ter, der bliver fremhævet i litteraturen er elevens færdigheder i forhold til:

Som det også fremgår af kapitel 3 anvender Olav Lunde det brede be-greb ”matematikvanskeligheder”, herunder indgår dog også dyskalkuli.Lunde anvender dertil begrebet kortlægning frem for test. Samlet set ermaterialet meget omfattende og består af tre bøger; A, B og C.I bog A beskriver Lunde forskellige teorier om elevers matema-tikvanskeligheder, der kan ligge til grund for det specialpædagogiske ar-bejde. Lunde gennemgår, hvad matematikvanskeligheder er i hans optik,og hvordan disse vanskeligheder hænger sammen med andre vanske-ligheder, som eleven eventuelt har. Han tager også fat på, hvordan mankortlægger elevens vanskeligheder i faget matematik, hvordan undervis-ningen kan organiseres, og hvilke undervisningsmæssige konsekvenserdet kan få.I bog B bidrager Lunde med en grundig vejledning i, hvordanfagligt relevante områder kan blive kortlagt, og hvordan testtageren kantolke opnåede resultater. Dertil er der forslag til tiltag, som testtagerenefterfølgende kan igangsætte ud fra kortlægningen. Ud fra en generelkortlægning kan testtageren udvælge de kortlægninger, denne vurdererrelevante for den enkelte elev.Bog C omfatter konkrete bud på, hvordan testtager eller lærerkan arbejde med elever med matematikvanskeligheder, herunder selvtillid,lærerforudsætninger, problemløsning og sproglige kompetencer.MICHAEL WAHL ANDERSEN: MATEMATIK FOR MIG

AndersensMatematik for miger en bearbejdning af Olav Lundes materialeRummelighed i matematik.Målgruppen er elever fra 2. klasse og ældre (7-9år og opefter). Ud over test eller kortlægninger består materialet af enrække hæfter med forskeligt indhold, som vælges på baggrund af kort-lægningen.Horsens Kommune har blandt andet anvendt testen og vurderer,at den er nemmere at bruge på indskolingselever end Olav Lundes op-rindelige materiale (Horsens Kommune, 2011).HILDE SKAAR DAVIDSEN, INGER KRISTINE LØGE, OLAV LUNDE, ELINREIKERÅS & TONE DALVANG: MATEMATIKKEN, INDIVIDET,OMGIVELSERNE (MIO)

en neurologisk forståelse af, at børn har en medfødt evne til at foretagenumeriske skøn, hvilket gør det relevant at arbejde med matematisk op-mærksomhed allerede fra to-års-alderen. Det drejer sig her om børnsevne til at skelne mellem størrelser og ikke formel matematik. Det kanvære begreber, som børn gennem hverdagsaktiviteter og lege gør sig er-faringer med, og som indeholder matematik.MIO er et redskab til systematisk observation af matematisk ak-tivitet, så pædagoger kan vurdere, hvilke tiltag der kan være behov for iforhold til at støtte børnenes matematiske udvikling. Materialet under-støtter pædagogers muligheder for at udvikle deres kompetencer til atobservere børns dagligdagsaktiviteter, der rummer matematik. Dennetidlige indsats kan være med til at motivere børnene og skabe grobundfor deres matematiske forståelse senere i livet. Der er også forslag til,hvordan arbejdet i daginstitutionen kan tilrettelægges, så børnene får mu-lighed for at videreudvikle sig.KIM FOSS HANSEN: MATEATIK GRUNDLÆGGENDE (MG), FÆRDIGHEDERGRUNDLÆGGEDE (FG) & POUL ERIK JENSEN, INGER-LISE JØRGENSEN,RASMUS ULSØE KÆR: MAT 1-9

Matematik Grundlæggende (MG), Færdigheder Grundlæggende (FG) ogMAT er standardiserede og meget udbredte klassetest.MG/FG er egnede til at indgå i diagnosticerende prøver til ma-tematikundervisningen i folkeskolen. De er målrettet elever i 0.-10. klasseog foregår på klasseniveau.41MG/FG bidrager med viden om klassensaktuelle standpunkt og giver overblik over, hvor klassens og den enkelteelevs præstation ligger på en skala fra ikke-indlært til sikkert-indlært. Der-til giver prøverne indblik i, hvilke typer af fejl eleverne begår samt bidra-ger med pædagogiske anvisninger til det fremtidige arbejde. Prøverne kandesuden anvendes til sammenligning med andre klasser på samme klasse-trin.MAT henvender sig til elever i 1.-9. klasse og bidrager med in-formation om, hvorvidt eleverne har tilegnet sig kundskaber og færdig-heder inden for hovedområderne tal og algebra, geometri og matematik ianvendelse. Opgaverne er progressive og bygget op efter trinmålene efter3. og 6. klasse og slutmålene efter 9. klasse. MAT-vejledningen indehol-der normer for, hvor meget man kan forvente, at eleverne kan inden forhvert delområde, samt hvor klassens standpunkt er i forhold til andre41. FG dækker de grundlæggende færdigheder og dækker 4.-9. klassetrin.

klasser på landsplan.42Det tilhørende webprogram MAT-elevplaner kangenerere individuelle elevplaner og analyser af klassens samlede stand-punkt inden for testede områder.Ifølge flere eksperter oplever mange lærere ikke, at disse test gi-ver et retvisende billede af de svageste elever, der muligvis har dyskalkuli.En del af kritikken går på, at MG-målinger ikke er udformet i overens-stemmelse med det, eleverne lærer i dag. En del lærere oplever også, atMG mangler anvisninger på, hvad de efterfølgende skal gøre for eleverne,når testresultatet foreligger. MAT søger at referere til uddannelsesmåleneog levere indsatsmateriale, men kun træningsmateriale ikke kompense-rende eller begrebsopbyggende materiale. Ser man på den tekniske ma-nual, er måleusikkerhederne ganske store på mellemtrinnetKIM FOSS HANSEN: MATEMATIK INDIVIDUELT (MI)

Matematik Individuelt (MI) vurderer 31 matematiske discipliner. Prøver-ne er samtalebaseret og giver et billede af, hvad eleven behersker, hvor-dan eleven tænker, og hvilke strategier eleven anvender. MI-prøverne eret værktøj til planlægning og tilrettelæggelse af undervisningsforløb, dertilgodeser elever med særlige behov inden for én eller flere af de discipli-ner, som matematik i skolen opdeles i. MI-prøverne består af et varieretantal trin, så de kan anvendes til elever fra 1. til 10. klasse. MI er altsåikke opdelt i klassetrin, men i 31 opgavehæfter med opgaver inden forhver af de 31 matematikfaglige discipliner. Prøverne er koblet tilMG/FG, således at man kan bevæge sig fra MG/FG til MI, hvor mankan starte fra det niveau, som eleven havde vanskeligheder med iMG/FG.BIRTHE HENRIKSEN & BERIT PEDERSEN: TIDLIG INDSATS I MATEMATIK(TIM)

Målgruppen er børn i 1.-2. klasse (ca. 6-9 år). Materialet er komplet ogstruktureret og består af flere hæfter, der dækker et helt TIM-forløb.TIM-forløbet består af identificering, testning, undervisning og evalue-ring med fokus på børn, der har behov for en særlig indsats i matematik.På baggrund af test tilbydes børene individuelt tilrettelagt TIM-undervisning 30-timer dagligt i ca. et halvt år, således at børnene kan føl-ge den almindelige undervisning i klassen.42. Disse normer er baseret på 1.800 besvarelser blandt knap 10.000 demografisk repræsentativeelever fra hele landet og på alle klassetrin.

Bjorn Adlers screeningsmateriale bliver mere og mere udbredt på skolerog hos PPR. En af årsagerne til den store udbredelse af Björn Adlers testkan være, at testen kan foretages af andre end psykologer modsat Wechs-lers test, som ellers er de mest udbredte i forhold til kognition.Adler har udviklet tre forskellige screeninger – Matematikscree-ning I, II, III – som er målrettet tre forskellige aldersgrupper. Matema-tikscreening I er målrettet 7-9figure, Matematikscreening II er målrettet11-15 årige, og Matematikscreening III er målrettet personer på 16 år ogopefter. Screeningen er ikke standardiseret.Adlers matematikscreening er først og fremmest udviklet medhenblik på at imødekomme et pædagogisk behov for at systematisereiagttagelser i en pædagogisk hverdag. Screeningen er tænkt som redskabtil individuel vurdering af den enkelte elev. Screeningsværktøjet kan bi-drage med informationer om forskellige matematiske vanskeligheder iforhold til underliggende kognitive processer, som eleven kan have pro-blemer med. Adler fremhæver vigtigheden af ikke alene at få indblik i det,eleven ikke kan, men også at få indblik i, hvad der ligger bag vanske-lighederne for at kunne planlægge eventuelle pædagogiske tiltag.Screeningen er opbygget som en tjekliste med et begrænset antalopgaver, som alle i en aldersgruppe forventes at kunne klare. Hvis elevenikke kan klare opgaverne, er det netop funktioner der vedrører opgaver-ne, der skal undersøges nærmere. Screeningen er bygget op på en måde,så den afdækker forskellige kognitive funktioner såsom praktiske hver-dagsopgaver, læse tid/klokkeslet, læse og skrive tal, talrækker, hukom-melse og planlægningsevner, geometriske figurer osv.I forlængelse af matematikscreeningen bidrager Adler medidébogenKognitiv træning i matematik,som rummer opgaveeksempler ogøvelser, der kan arbejdes med, efter at eleven har gennemgået matema-tikscreeningen.43Ifølge flere eksperter er der mange praktikere, der oplever, atscoringen af testen er meget vanskelig og ofte også giver et billede, somikke stemmer overens med andre test samt med personens egne beret-ninger.

Adlers screening blev blandt andet anvendt i CSV SydØstfyns udvik-lingsprojekt om talblindhed (2010). 85 personer med formodet talblind-hed blev testet, hvor næsten alle deltagere viste tegn på store vanske-ligheder i matematik. Der viste sig imidlertid ikke noget entydigt billedeaf gruppen. Erfaringen var, at testresultaterne var meget afhængige aftesttageren og af dennes skøn og tolkning. Der er kun to muligheder iscoringen af testen – enten fejl (0) eller accepteret (x). Undervejs i under-søgelsesfasen blev projektgruppen usikker på, hvordan resultaterne fraAdlers screening skulle tolkes. Flere af testpersonerne blev derfor ogsåundersøgt med delprøver fra andre test, og enkelte fik supplerende ogmere omfattende testrunder (CSV SydØstfyn, 2010).REGION NORDJYLLAND

Region Nordjylland startede et treårigt projekt i 2012, hvor de ligeledeshar ladet sig inspirere af Björn Adler. Projektet ligger i forlængelse af ettidligere projekt, hvor der blev udviklet screeningstest for dyskalkuli medopfølgende støttetiltag. I projektet ligger desuden et mål om, at dys-kalkuli er klart afgrænset, og kriterierne for funktionsnedsættelsen erpræcist defineret på baggrund af eksisterende international litteratur ogløbende resultater i projektet. Projektet er målrettet til elever på ung-domsuddannelserne og som noget nyt også til elever i 8., 9. og 10. klasse-trin med hensigten om også at nå de elever, der kunne ”tabes”.Projektet anvender først en kort test som screeningsværktøj,hvor en større gruppe elever (typisk en klasse ad gangen) screenes samti-dig. Den korte test skal indikere, om eleven har matematiske udfordrin-ger, som eventuelt skal undersøges nærmere, og hvis det er tilfældet, bli-ver den korte test suppleret med en lang test for yderligere at belyse,hvor udfordringerne ligger.Den korte test findes i to udgaver (henholdsvis A og B), så ele-ver, der sidder ved siden af hinanden, ikke umiddelbart kan skrive af ef-ter hinanden. Den korte test består af 4 A4-ark og indeholder 5 deltest.Hver deltest udløser et antal point, som kan indikere, om eleven harproblemer. Deltestene omfatter: 1) oplæsning af tal, 2) talfølger, 3) sy-stemer i figurer, 4) tallinjer og 5) små regneopgaver.Den lange test er beregnet til at teste de elever, der er udvalgt påbaggrund af den korte test (ovenstående) og efter aftale med elevens ma-tematiklærer. Testen foregår individuelt, og det bliver frarådet, at testlæ-

reren er elevens matematiklærer. Hvis testen viser, at eleven ikke er tal-blind, kan den bidrage med viden om, hvorfor eleven blokerer for ma-tematik. Den lange test består af 36 spørgsmål, som bliver afsluttet meden samtale, der skal afdække elevens holdning til matematik og ele-vens ”matematikhistorie”. Undervejs nedskriver testlæreren observatio-ner, såsom hastighed, fingertælling, afvigende blyantsgreb (”klofatning”),behov for gentagelse af instrukser mv. Den lange test er inspireret afBjørn AdlersKognitiv træning i matematik(2004) og er bygget op om 10temaer:1.Tal/cifre.Problemer med at arbejde med tal og cifre kan vise sigsom vanskeligheder med at skrive, læse eller kopiere tal og cifreog endvidere ved manglende forståelse for, hvorledes cifre kankombineres til forskellige tal. Problemer med tal/cifre kan ogsåvise sig ved problemer med at organisere tallene i rækkefølge(som sammenligninger eller klassifikationer).2.Talbegrebet.Vanskeligheder ved at håndtere talbegrebet viser sigisær som vanskeligheder med den sproglige forståelse af vigtigematematiske grundbegreber fx størrelser som begreberne mange– flere – flest eller lille – mindre – mindst.3.Antalsopfattelse.Vanskeligheder med antalsopfattelse viser sig ved,at eleven på forståelsesplanet ikke kan koble mellem tallet og an-tallet (at erstatte antallet af enheder til en helhed/tallet som sym-bol).4.Skema for tal.Handler om at forstå afstanden mellem heltal på entallinje. Vanskeligheder her viser sig ved problemer med hurtigtat hente cifferfakta frem om, hvilket tal der er størst. Vanske-lighederne kan også vise sig som problemer med at skelne mel-lem tal, som bliver sammenlignet.5.Arbejdshukommelse/opmærksomhed.Elever med vanskeligheder herhar ofte problemer med at fastholde flere informationer samtidig.Vanskeligheder afspejler sig ved problemer med hovedregning,men også forskellige former for problemløsning. Ofte vil vanske-ligheder komme til udtryk ved, at eleven udviser ujævne præstati-oner, og deres vanskeligheder medfører, at deres arbejde kan væ-re præget af ”sjuskefejl”.6.Perception.Perceptionsvanskeligheder kommer til udtryk ved fxproblemer med at skrive cifre og tal eller tegne geometriske figu-

rer. Det kan også være usikkerhed omkring retningsangivelser el-ler ved, at man har vanskeligheder med formopfattelse (at opfatteforskellige formers indbyrdes størrelse). Perceptionsvanskelighe-der kan også vise sig ved vanskeligheder med at diskriminere mel-lem forskellige lyd- og sanseindtryk. Det sidste medfører, at ele-ven kan blive opfattet som afledelig eller uopmærksom.Spatial tænkning(abstrakt). Spatial tænkning fremtræder først tyde-ligt omkring 12-års-alderen og indebærer evnen til – visuelt – atforestille sig ting og hændelser og foretage sammenligninger.Vanskeligheder kommer til udtryk ved problemer med at ”holdeden røde tråd” i et arbejde. Eleven mister let fokus og har brugfor megen hjælp for at kunne organisere og strukturere sit arbejde.Planlægning.Vanskeligheder med at forudse og planlægge skyldesmanglende overblik og problemer med at udskille forskellige se-kvenser i en matematikopgave.Tidsopfattelse.Tidsopfattelse er en evne, der løber parallelt medandre evner som fx rumopfattelse, planlægningsevne og logisktænkning samt opmærksomhed og koncentrationsevne. Har ele-ven vanskeligheder med tidsopfattelse, vil det blandt andet kom-me til udtryk ved problemer med at angive tid, planlægge tidsfor-bruget ved opgaveløsning, følge et hændelsesforløb i en matema-tikopgave samt vanskeligheder med at håndtere og bearbejde in-formation. Ofte vil eleven samtidig have vanskeligheder med for-ståelsen af tallenes størrelse og delt opmærksomhed (evnen til attænke på to ting samtidig og foretage sammenligninger). I til-knytning hertil er det sandsynligt at finde, at der er vanskelighe-der med aflæsning af et analogt ur.Logik og problemløsning:Logisk tænkning handler om evnen til attænke sig frem til en løsning i en veldefineret sekvens. En forud-sætning for udviklingen af logisk tænkning er evnen til at reflekte-re over, hvorledes en opgave er løst (hvad et rimeligt svar er,hvordan sammenhængen mellem et rimeligt svar og det angivnesvar er, hvordan man kan og skal gøre, hvis der er forskel på detrimelige svar og et angivet svar).44

Lindenskov & Weng (2013) har udgivet bogenMatematikvanskeligheder –tidlig intervention.Bogen fungerer som et praktisk redskab til at kortlæggeog styrke elevers matematiske begrebsudvikling inden for ti basale ma-tematiske områder. For hvert af de ti områder bidrager bogen med kon-krete og varierede forslag til at kortlægge elevers matematiske begrebs-udvikling samt konsoliderende og videre læring. Denne opbygning skullegøre det muligt at tilpasse matematikstoffet til den enkelte elevs forud-sætninger og behov. Bogen indeholder også en screeningstest, der kanbruges indledende til at afdække elevens forudsætninger, potentialer, be-hov og motivation. Bogens tilgang bygger på forfatternes begrebs-valg ”regnehuller”.45Bogen har visse lighedspunkter med Emerson &Babties dyskalkuli-vurdering”.MICHAEL WAHL ANDERSEN OG MICHAEL POULSEN: TRINMÅL IMATEMATIK – EVALUERING EFTER 3. OG 6.

måen og matematiske udvikling. I materialet er elev-selvvurdering ind-bygget. Formålet er at vurdere elevens faglige formåen og matematiskeudvikling. Materialet har karakter af både at være summativt og formativt,idet test i dette materiale ikke altid giver indblik i løsningsprocessen. Detvil sige, at der både er en vurdering af, om en minimumskompetence eropfyldt (summativ) og et formål om at styrke elevens faglige udvikling(formativ). Tanken er, at materialet bliver anvendt formativt i klassenmed henblik på at tilrettelægge undervisning for den enkelte elev.KIRSTEN TØNNESEN: TJEK OG TRÆN 4. OG 5.

Målgruppen er børn på 4. og 5. klassetrin (ca. 9-12 år), men materialetkan anvendes på andre klassetrin og i specialklasser, idet testen ikke sig-nalerer klassetrin. Evalueringen har en formativ karakter, hvor elevernehar mulighed for at være aktive og løse opgaver samt deltage i klassensarbejde. Materialet består af både en testdel og en træningsdel, hvoraftræningsdelen arbejder på tre niveauer. Læreren placerer eleverne på ni-veauer efter en grundig og differentieret for-test.GUDRUN MALMER: ANALYSE AF LÆSEFORSTÅELSE I PROBLEMLØSNING(ALP)

Gudrun Malmer har udviklet et analysemateriale, som kan bidrage meden indikation af, om det er på grund af manglende sproglig kompetence,at elever har svært ved klare problemløsning. Forkerte og uholdbare løs-ninger i matematik kan ifølge Malmer bero på mangler i den sprogligeudvikling og ikke nødvendigvis i evnen til at udføre forskellige regneope-rationer. Analysematerialet kan anvendes som et supplement til de andretest, hvis der er mistanke om, at elever har vanskeligt ved problemløs-ningsopgaver. Opgaverne er opdelt i otte trin med stigende sværhedsgrad.I hver opgave indgår 10 eksempler med spørgsmål på A-, B- og C-niveau.Opgaverne vurderes i forhold til den aktuelle elev eller klasse. ALP ertænkt som et materiale til pædagogisk afdækning og kan bidrage medinformationer om sammenhænge mellem læsefærdigheder, læseforståelseog de matematiske grundbegreber og matematisk-logisk tænkning.Som vi ser det, er Gudrun Malmers analysemateriale ikke direkteanvendeligt i forhold til at identificere dyskalkuli. For eksempel pointererButterworth (1999), at dyskalkulikere ofte kan forstå talord (fx en, to, tremv.), men ikke tal (fx 1, 2, 3 mv.) Imidlertid kan Malmers materiale bi-drage med andre informationer, som kan være med til at udelukke dy-

skalkuli og pege i retningen af en anden type vanskelighed, der kan sættesind overfor inden for den brede vifte af matematikvanskeligheder. Lunde(2006) har fokus på matematikvanskeligheder i bred forstand. Han frem-hæver, at sprogfærdigheder er den vigtigste forudsætning for at lære ma-tematik. Endvidere fremhæver han, at det netop er sammenhængen mel-lem dagligdagens sprog og matematikken, der kan gøre det lettere forbørn at relatere til matematik.I forhold til de test, der fokuserer på matematikvanskeligheder,er der konsensus om at undersøge følgende aspsekter:

WISC48er en intelligenstest for børn i alderen 6-16 år, og den må kunudføres af psykologer. Den bliver brugt i en lang række sammenhængefra vurdering af børn i PPR-regi til neuropsykologiske udredninger.WISC bidrager med en overordnet intelligensscore og giver samtidig og-så information om barnets styrker og svagheder vedrørende indlæring.Det betyder, at testen giver information om barnets generelle potentialeog samtidig indikerer, hvilken undervisningsstil der formentlig vil væreeffektiv. En generel intelligenstest, som er baseret på en gennemsnitssco-re alene, vil være vildledende, hvis barnet har særlige vanskeligheder så-som dyskalkuli. Typisk vil en person med dyskalkuli have en lav scoreved de tal-orienterede delprøver, mens den verbale del-IQ er højere endnormalt. Det er ofte den dramatiske forskel, der tydeliggør problemet ogviser mere specifikt, hvor problemet har rod.WISC består af 15 delprøver og skalaens struktur er baseret påen inddeling af de 15 delprøver i følgende fire indekser:1. Verbal forståelse med delprøverne lighed, ordforråd, omtanke,information og ordræsonnering2. Perceptuel ræsonnering med delprøverne blokmønstre, billedka-tegorier, matricer og billedfuldendelse3. Arbejdshukommelse med delprøverne talspændevidde, bogstav-tal rangordning og regning4. Forarbejdningshastighed med delprøverne kodning, symbolsøg-ning og udstregning.For at beregne IQ for hele skalaen (HIK) må kun to kernedelprøver er-stattes af supplerede delprøver. Det er også muligt at beregne GenerelFærdighed Indeks (GFI), som er et sammensat mål på generelle evner,som er mindre følsom over for påvirkning af arbejdshukommelse og for-arbejdningshastighed sammenlignet med HIK. For at beregne GFI bliver47. Se eventuelt også http://www.pearsonassessment.dk/dk/Klinisk-psykologi/Produkter/Utveckling-och-begavning/WAIS-IV/.48. Den nyeste og fjerde udgave fra 2003 hedder WISC-IV (dansk version 2010).

opgaverne kombineret, så de afspejler de fire overordnede kognitivefunktionsområder: sproglig forståelse, perceptuel organisation, arbejds-hukommelse og forarbejdningshastighed. De fire kognitive funktions-områder giver tilsammen GFI og kan i nogle tilfælde give et mere præcistudtryk for barnets formåen end den totale IQ49(Emerson & Babtie,2010).Hale m.fl. (2003) foretog en neuropsykologisk analyse af WISC-resultater hos elever med matematikvanskeligheder med det formål atpåvise en sammenhæng med venstre hemisfærefunktioner. De mener atkunne påvise sådanne sammenhænge, men advarer mod, at det anvendesved diagnose af læringsvanskeligheder hos skoleelever. Hale m.fl. påpe-ger også, at forskningen viser, at tiltag næppe er lige effektive for allebørn, da deres effekt vil afhænge af barnets kognitive funktionsprofil.En af de mest kendte kognitive profiler er Bannatynes, der byg-ger på WISC. Han opstiller fire faktorer (Lunde, 2012):1. Spatial bestående af færdiggørelse af billeder, puslespil og møn-stertegning2. Konceptuel bestående af ræsonnement, ligheder og ordforståelse3. Kundskab bestående af information, regning og ordforståelse4. Sekventiel, bestående af talhukommelse, tegneserier og kodning.Ifølge Bannatyne skal den spatiale faktor være højere end den sekventiel-le, hvilket forudsætter, at en given læringsvanskelighed har en veldefine-ret profil. Andre forskere50har afvist en sådan profil og påpeger, at enprofil som fx Bannatynes er uden værdi ved diagnosticering af lærings-vanskeligheder hos enkeltindivider. De mener, at visse tendenser kanpåvises, men kun på gruppeniveau (Lunde, 2012).I Norge bruger man ofte en kombination af WISC og forskelligematematikprøver. Det er dog uklart, i hvor høj grad WISC og prøvernekan anvendes som grundlag for tiltag (Lunde, 2006).THE WECHSLER ADULT INTELLIGENCE SCALE (WAIS)

fleste psykologiske undersøgelser og vurderinger. Testen vurderer intelli-gens og kognitive funktioner hos unge og voksne i alderen 16-90 år ogmå som WISC og WPPSI kun udføres af psykologer.Som WISC består WAIS af de samme 10 kernedelprøver og 5supplerende delprøver, som er inddelt på samme måde som i WISC i fireindeks: verbal forståelse, perceptuel ræsonnering, arbejdshukommelse ogforarbejdningshastighed. Ligesom med WISC kan man også beregne IQfor hele skalaen (HIK) og det supplerende mål General Ability Index(GAI) (hedder Generel Færdighed Indeks (GFI) i WISC), som er etsammensat mål for kognitive evner. Man kan dertil beregne forskelligeproces-scorer for delprøverne blokmønstre, talspændvidde og bogstav-tal-rangordning. Disse proces-scorer giver information om, hvilke kogni-tive processer der bidrager til præstationen på de respektive delprøver.Tidligere har man for både WISC og WAIS opdelt skalaen i enverbal IQ og en performance-IQ, hvilket man er gået bort fra.52MOGENS HANSEN, SVEND KREINER, CARSTEN ROSENBERG HANSEN:CHILDRENS PROBLEMSOLVING (CHIPS)

Inden for dyskalkuli-området har Children’s Problem Solving (CHIPS)også været anvendt, dog i et beskedent omfang.53CHIPS vurderer børnskognitive udviklingsniveau. Det vil sige, at den tester, hvordan barnettænker og løser problemer og opgaver på det givne tidspunkt. CHIPS ertænkt som et værktøj til at planlægge undervisning og ikke en intelligens-test. Opgaverne bygger på almen kognitiv udviklingsteori. Hvordan op-gaverne bliver løst, giver en indikation af, hvor i udviklingsforløbet detenkelte barn befinder sig. CHIPS henvender sig til børn mellem 3-18 år.Testen er visuel og kræver derfor ikke læsefærdigheder. Den findes i treforskellige udgaver: til skolebørn individuelt og som klasseprøve; til små-børn (5-7 år); og mini-CHIPS til de helt små børn (3-4 år). Testen er ikkematematikfaglig og kan derfor anvendes generelt.De kognitive test vurderer børns kognitive udvikling, – evner og– niveau. Fokus er på følgende punkter:

Dyskalkuli og matematikvanskeligheder er ikke det samme fænomen.Dyskalkuli er udtryk for neurologisk funktionsnedsættelse (Butter-worth; Emerson & Babtie; Andersen; Skaar, Løge, Lunde, Reikerås& Dalvang), men visse perspektiver på dyskalkuli vægter også psy-kologiske, sociale og/eller didaktiske aspekter.Diagnoser og test af dyskalkuli skal kunne føre til en relevant indsatsog mulighed for at lære kompenserende strategier.Test kan bidrage med viden om elevernes færdighedsniveau ogeventuelle vanskeligheder, således at der kan sættes ind overfor dissevanskeligheder.

Om udgangspunktet for test er matematikvanskeligheder bredt ellerdyskalkuli snævert.Om hvorvidt formålet med testen er at udelukke andre typer van-skeligheder for at finde frem til, om der er tale om dyskalkuli, ellerom det drejer dig om at identificere andre vanskeligheder, hvis derikke er tale om dyskalkuli.Om hvorvidt fokus specifikt skal være på talfornemmelse (tal- ogmængdeforståelse) eller matematiskvanskelighed med et mere holi-stisk perspektiv på barnets udvikling og trivsel.Hvilke målgrupper de forskellige dyskalkuli-test henvender sig til(målgrupper fra 2-5 til 3-18 år).Tilpasning af test. Litteraturen omfatter alt fra skræddersyede test afindividuelle børn til afklaring af klassens generelle standpunkt.

Vanskeligheder ved at opremse tal uden at bruge objekter (fx fingre)Vanskeligheder ved at tælle forlæns og baglænsVanskeligheder ved at sætte tal i rækkefølgeVanskeligheder ved enkle sammenligninger af tal (talmæssig størrel-se og fysiske størrelse)Vanskeligheder ved simple regnestykker (addition, subtraktion, mul-tiplikation og division) med etcifrede talPrimitive additions- og subtraktionsstrategier (fx fingertælling)Vanskeligheder ved fingertælling (eleven tæller fx langsomt og unøj-agtigt)Vanskeligheder ved simpel sprog- og begrebsforståelse inden formatematikken.

Test vil således i mange tilfælde belyse noget mere end den ”rene” dys-kalkuli. En validering af test kan ske ved at undersøge, i hvilket omfangforskellige test vil udpege de samme elever som dem, der har dyskalkuli.En sådan validering er vi dog ikke stødt på i forbindelse med vores litte-raturgennemgang.Fra alle sider er der enighed om, at testene bør føre til handle-muligheder og -anvisninger, så fx skolen har mulighed for at igangsætteen relevant indsats. I det følgende kapitel skal vi derfor se nærmere på destøtteformer, der bliver fremhævet i litteraturen.

STØTTEFORMERDiagnoser og test har til formål at specificere en behandling eller et tiltag.Hvis en diagnose og en test ikke kan lede frem mod en indsats, har denringe værdi. Uden en særlig indsats vil mange børn, unge og voksne, sommuligvis har dyskalkuli, kæmpe med basale regneprocesser, hvilket kanhave negative følgevirkninger i deres uddannelses- og hverdagsliv.I dette kapitel skal vi derfor se nærmere på støtteformer. Kapit-let omfatter både de støtteformer, der kommer i anvendelse som konse-kvens af testresultater54og støtteformer, der i øvrigt er omtalt i litteratu-ren. Dertil vil vi belyse, om der er forskning, der støtter, at de anvendtestøtteformer har en virkning i forhold til dyskalkuli, herunder en inklude-rende og udviklende virkning.Som tidligere nævnt har vi i de fleste tilfælde ikke haft direkteadgang til konkrete test og dermed heller ikke de støtteformer, derkommer i anvendelser som konsekvens af testresultater. Dette afspejlersig i vores beskrivelse af de konkrete aktiviteter, herunder hvad disse ak-tiviteter specifikt træner, og hvilken målgruppe aktiviteterne henvendersig til (alder og klassetrin). Vi har derfor valgt, at beskrive støtteformernemere generelt snarere end at beskrive de specifikke støtteformer, der føl-ger af konkrete test (som vi fx har gjort med testbeskrivelserne i kapitel4).54. Jf. kapitel 4.

Når først der er konsensus om, hvilke specifikke regnevanskeligheder derer tale om, og hvad der skal læres, må det specificeres, hvordan det skallæres. En test er et redskab til at kunne identificere vanskeligheder, somkan give særlige undervisningsmæssige behov og på den baggrund tilbyderelevant undervisning. Det er derfor vigtigt, at en given test bliver ledsa-get af anvisninger til, hvordan udredte elever kan hjælpes videre, oghvordan en udbytterig matematikundervisning for alle (forstået som heleklassen) kan tilrettelægges. En del af den litteratur, der indeholder test,giver ligeledes bud på, hvordan der kan følges op på de enkelte test.55I de følgende afsnit vil vi for det første belyse, hvornår en ind-sats for mennesker med dyskalkuli kan blive igangsat. Dernæst vil vi be-lyse, hvordan en indsats kan foregå.TIDLIG INDSATS

Litteraturen indikerer, at matematik allerede i førskolealderen kan tænkesind i børnenes legeaktiviteter, hvormed det er muligt at reducere senerevanskeligheder med tal. I litteraturen og blandt eksperter fremgår det, aten tidlig, målrettet og langsigtet indsats giver elever med dyskalkuli mu-lighed for at få relevant støtte. Dertil kan eleverne få mulighed for fortsatat deltage i den almindelige undervisning sammen med deres klassekam-merater. Flere eksperter mener, at der især skal være respekt for denlangsigtede indsats, som kan skabe motivation for faget gennem heleskoleforløbet.Som nævnt i kapitel 4 er der flere eksperter, der påpeger, at detførst giver mening at diagnosticere børn med dyskalkuli omkring 4. klas-setrin. Samtidig så vi i samme kapitel, at de test, vi er stødt på, primærthenvender sig til skolebørn. Hvis vi tager udgangspunkt i denne aldersaf-grænsning, vil det også sige, at indsatsen først for alvor kan målrettesefterfølgende. Indtil børnene når 4. klassetrin, er der imidlertid mangemuligheder for at observere dem, der er i risiko for at komme i vanske-ligheder. Som det fremgår i kapitel 4 kan mange test eller kortlægningerallerede anvendes i førskolealderen.56Observationer kan dermed foregå iforbindelse med, at matematikken bevidst og struktureret integreres ibørnenes hverdag, fx i forbindelse med lege og hverdagsaktiviteter.55. Se evt. den skematiske oversigt i bilag 1.56. Se evt. den skematiske oversigt i bilag 1.

Lundberg & Sterner (2009) påpeger, at aktuel forskning viser, atdet er vigtigt allerede i børnehaveklassen at være opmærksom på oghjælpe børn, som af den ene eller anden grund har tilbøjelighed til at ud-vikle regnevanskeligheder.Butterworth (1999, 2003, 2004) er blandt andre fortaler for, atbørn har en medfødt intuitiv talfornemmelse, forstået som tal- ogmængdeforståelse. Han fremhæver, at forskning viser, at børn alleredefra spædbarnsstadiet har en mængdeforståelse og evne til at skelne mel-lem to størrelsesordener. Med denne medfødte ”startpakke” bygger bør-nene deres kulturelle redskaber, såsom talord, taloperationer og aritmeti-ske procedurer. Dyskalkuli vil derfor tidligt komme til udtryk, når børnhar vanskeligheder med numeriske begreber (numerical concepts), særligtmængder, herunder tælling og sammenligning af to mængder. I Butter-worths dyskalkuli-screener57er målgruppen børn i alderen 6-14 år. Imid-lertid kan forældre, pædagoger og andre relationer igangsætte aktiviteter,der stimulerer meget basale aritmetiske aspekter langt tidligere.Ifølge Magne (1994, 2004) begynder små børn spontant at skabematematiske erfaringer. Først sensomotorisk, siden abstrakt operationelt.Elevens sociale kompetencer udvikles allerede inden skolens begyndelse ihverdagslivet med familie, venner og nærmiljø. Det er ifølge Magne net-op i sådanne hverdagssituationer, at matematik indgår og kan udbygges.Lunde (2008) påpeger, at matematikken indeholder fire forskelli-ge væsentlige sider: regnefag, sprogfag, tænkefag og kontekstfag. Lundehar ud fra denne inddeling udformet en arbejdsmodel (figur 5.1), der hartil formål at forebygge matematikvanskeligheder, da den giver et fysiskbillede af de mulige sammenhænge, der er mellem de centrale elementer imatematikken.

Denne model skal skabe et grundlag for den undervisning, der foregår iskolen, og dette grundlag skal etableres i børnehaven. I børnehaven erdet op til pædagogerne at synliggøre matematikken og inddrage den ilegen, rutinerne og emnerne, der tages op, og det er herunder, Lundemener, at hans model bliver anvendelig.Lunde (2010) påpeger, at det er muligt at foretage screeninger afførskolebørn og dermed forebygge udviklingen af matematikvanske-ligheder. I den forbindelse fremhæver han screeningsværktøjet MIO58.Lunde pointerer, at nyere forskning59viser, at når man ser på, hvordanbørn læser tal, forstår og bruger etcifrede tal og mental addition af etcif-rede tal, så kan det give et godt billede af, hvor børnene er i deres mate-matiske udvikling. Dertil fremhæver han, at 60-80 pct. af førskolebørn,som senere udviklede matematikvanskeligheder, kunne identificeres vedhjælp af så enkle test/observationer som ovennævnte i førskolealderen.Ifølge Lunde (2006) kan børn allerede i 2-3-års-alderen arbejde med atlære basale matematiske aspekter.58. Se mere om MIO i kapitel 4 eller den skematiske oversigt, bilag 1.59. Lunde fremhæver blandt andet Mazzocco & Thompson (2005) samt Morgan m.fl. (2009).

Blandt andre problematiserer Lunde (2006) og Munn & Reason(2007), at elevens matematikvanskeligheder ofte opfattes som noget sta-bilt, som ”eleven har”.60Munn & Reason (2007) advarer imod, at manforstår dyskalkuli som en barriere, der hindrer børnene i at udvikle sigmatematisk og opnå en forståelse af matematik. Munn & Reason påpegerat børn godt kan udvikle en matematisk forståelse, da matematikudvik-ling netop ikke er lineær. Ifølge Munn & Reason er det således muligt atudvikle en konceptuel forståelse på nogle områder, som således vil kunnekompensere for langsom udvikling på andre områder.Schilling & Proching (1991) fremhæver, at barnet kan forme ogskabe med ting fra 2-3-årsalderen, hvormed barnets fantasi og forestil-lingsevne bliver sat på prøve. I omgangen med genstande og legetøj be-gynder barnet at skelne mellem orden og kaos, og det skaber helheder ogødelægger dem.Samlet set understøtter litteraturen en tidlig og forebyggendeindsats. En tidlig indsats er her forstået som en indsats i førskolealderen,og denne kan allerede påbegyndes, når børnene er omkring to år. Detbliver imidlertid også understreget, at der bør være opmærksomhed på,at børns udvikling ikke er lineær, og at børn lærer i forskellige tempi. Iforlængelse heraf er næsten alle test målrettet skolebørn. Vi antager der-for, at en egentlig dyskalkuli-indsats med udgangspunkt i test eller scree-ninger ikke vil være aktuel, før barnet er startet i skole. Dog antager visamtidig, at barnets relationer (forældre, pædagoger m.fl.) kan påbegyndeen tidlig og forebyggende indsats langt tidligere – omkring to-års-alderen.ANVENDTE STØTTEFORMER

giver mening for børnene. Børn kan allerede i førskolealderen lære stra-tegier og særlige teknikker til at håndtere tal og dermed lære strategier tilat leve med dyskalkuli. Flere eksperter fremhæver, at god og inkluderen-de matematikundervisning stimulerer og aktiverer flere sanser fx vedbrug af ord og billeder, fysisk aktivitet, hverdagssituationer og lege mv.Schilling & Proching (1991) bidrager med et hæfte fuldt af kon-krete forslag til forskellige sanselege, hvor matematikken bliver inddraget.I hæftet er der specifikke læringsmål, såsom mængdelære, grupperinger,volumen, talfornemmelse mv. Forfatterne argumenterer, at barnet gør sigsine erfaringer i et vekselspil med omverdenen – først og fremmest gen-nem leg. Inden for neuropsykologien er det ligeledes anerkendt, at san-sebaserede aktiviteter kan fremme læring, idet der kan være en sammen-hæng mellem forstyrrelser i sansebearbejdning og lærings- og trivselsvan-skeligheder (Ayres, 2007). Dette må vi dog antage især gør sig gældendeinden for matematikvanskeligheder bredt. Dog kan vi antage, at det kanhave betydning, når dyskalkulikere skal lære at anvende kompenserendestrategier.Gudrun Malmer (2001) argumenterer for, at logisk tænkning fårmeget større betydning og plads, end den får i dag. Grundforudsætnin-gen herfor er ifølge Malmer en kombination af matematisk og sprogligkompetence. Hun påpeger, at en af de alvorligste misforståelser er dentidlige indførelse af symboler, da eleverne endnu ikke har forstået me-ningen med dem. Ifølge Malmer burde man i højere grad sætte tid af tilmundtlig matematik og handlingsmatematik. Elevens erfaringer skal iføl-ge Malmer aktualiseres, og eleverne skal sætte ord på det, de ser og gør,da de igennem italesættelsen ”tvinges” til at tænke over, hvordan meka-nismerne fungerer. Hun fremhæver, at det er vigtigt at tage udgangs-punkt i elevernes hverdag og anvende eksempler, som de kan relatere til.Hun påpeger i den forbindelse, at mange elever er dygtige logiske tænke-re, men at de kan have svært ved at følge de rammer og formler, somlæreren stiller op for korrekt opgavebesvarelse.Magne (1994, 2004) argumenterer, at legedidaktik er anvendeligog effektiv for mange førskolebørn og også for ældre børn og unge. Hanmener, at børn lærer mere af fysiske aktiviteter end blot fra sprog. Hanpointerer, at der skal skabes konkrete erfaringer, da disse erfaringer ergrundlaget for tænkning og dertil, at tænkning medfører, at sproget ska-bes. Han fraråder samtidig, at yngre børn skal have øvelser i cifferskriv-ning, da de i begyndelsen har meget svært ved at forme tal. Det er fint, at

de blot møder og ser cifre. Magne (1994) bidrager med forskellige ek-sempler på legeaktiviteter for børn med matematikvanskeligheder. Handeler legeaktiviteterne op i fire hovedområder: 1) P-området, som ersprogopfattelse og problemløsning, fx hvor kvantitetsord som ”al-le”, ”mange”, ”ingen”, ”nogle”, ”få” osv. bliver inddraget; 2) T-området,som er talforståelse, hvor forskelle i mængder identificeres, fx ved at op-stille forskellige objekter; 3) G-området, som er geometri, rumopfattelse,fx øvelser med balancen, kropskontrol og overblik over kropsdele; 4)ASMD-området, som er de fire regnearter. Vi antager, at hovedområde 2(talforståelse) mere specifikt henvender sig til dyskalkulikere.Magne (1994; 2004) advokerer for, at selve matematikken skalvære baseret på det, han kalder livsmatematik, hvor matematikken tilpas-ses elevernes virkelighed. Han argumenterer for, at man i højere gradskal tage udgangspunkt i børnenes hverdag og gøre matematik relevantog meningsfuld. Ifølge Magne er elevens læring baseret på, at eleven ”ak-tivt skal bearbejde” og ”frivilligt søge”. Samtidig skal eleven udvikles i ogigennem et socialt netværk. Læreren skal derfor planlægge elevernes akti-viteter ved hjælp af praktiske problemer, det vil sige virkelige handlingermed ingredienser af matematisk problemløsning.Lunde (1994, 2006) påpeger, at et hovedprincip i matematik forførskolebørn må være at videreføre elementer inden for tal- og mængde-forståelse. Lunde (1994) omtaler herunder fem matematiske principper,som børn synes at have et implicit kendskab til: 1) en-til-en-princippet(hvert element i en mængde kan kun give et bestemt mærke, fx ”3”, éngang), 2) stabil orden (bestemt rækkefølge), 3) kardinalprincippet (detsidste mærke i en række er symbolet for antal elementer i mængden), 4)abstraktionsprincippet (en hvilken som helst type objekter kan tællessammen for at finde antallet); 5) irrelevant-orden-princippet (tælle-rækkefølgen er ligegyldig, så længe de andre regler følges).61Lunde frem-hæver, at selv meget små børn synes at have en intuitiv forståelse afovennævnte elementer, og at børn bruger matematik for at mestre omgi-velsernes krav, fx i leg.Endvidere fremhæver Lunde (2006, 2008b), at en vej til at hjælpeelever med regnevanskeligheder kan være at lære dem generelle strategier,så de kan orientere sig i problemområder, det vil sige, at systematisereinformationen. Lunde mener yderligere, at forholdet mellem sprog og61. Magne henviser i den forbindelse til Strass & Curtis, 1981; Groen & Resnick, 1977 samt Gelman& Meck, 1983.

matematik skal styrkes, idet sprogfærdigheder ifølge Lunde er den vigtig-ste forudsætning for at lære matematik. Dertil påpeger Lunde, at når ele-ven laver regnefortællinger, er det netop sammenhængen mellem daglig-dagens sprog og matematikken, der gør det lettere for eleven at relateretil matematikken.Samlet set peger litteraturen i retning af, at alle barnets sanser såvidt muligt bliver inddraget i læringen. Dette kan lade sig gøre ved at in-tegrere matematikken i barnets lege og hverdagsaktiviteter. Når barnetanvender matematik i lege og hverdagsaktiviteter, kan det være med til atforebygge senere regnevanskeligheder, ved at barnet tidligt får mulighedfor at udvikle strategier til at håndtere vanskelighederne.UNDERVISNING

I litteraturen er undervisningens indhold og form centrale temaer. Litte-raturen anbefaler, at læring foregår på flere niveauer: klasseniveau, grup-peniveau og individuelt niveau. Dertil er det gennemgående, at indholdeter bredt, men særligt med vægt på at træne talfornemmelsen. Dertilkommer italesættelse af strategier og læring af kompenserende strategier.Læring på klasse- og gruppeniveau giver muligheder for mundt-lige præstationer med interaktiv læring, hvor elever med dyskalkuli harmulighed for at lære af de andre elever. Dette kan foregå ved, at elevenhører, hvordan de andre i klassen trinvis gennemgår forskellige regne-processer. Det kan også være en hjælp for eleven selv at præsentere ogdermed italesætte sine handlinger. Denne form kan dog i nogle tilfældeskabe øget angst hos elever med dyskalkuli, idet der kan opstå udtaltpræstationsangst i tilfælde, hvor de selv skal præstere mundtligt. Læringpå gruppeniveau kan muligvis reducere eventuel præstationsangst hoseleven, som måske føler sig mindre udsat i en lille (eventuelt differentie-ret) gruppe. Læring på individniveau giver eleven mulighed for at arbejdeselvstændigt og afprøve egne og tillærte strategier samt udvikle strategier.CSV har med støtte fra Undervisningsministeriet afprøvet ogudviklet undervisningsmetoder og -materialer i samarbejde med førendeeksperter på området. 85 børn, unge og voksne blev testet med forskelli-ge prøver for at afdække, om de kunne have talblindhed som deres pri-mære vanskelighed. Forskningsprojektet på CSV omhandler dog primærtvoksne. Målet var at finde ud af, hvordan undervisningen tilrettelæggesmest hensigtsmæssigt for talblinde. CSV’s egne kursister og kursisterudefra (blandt andet VUC) har medvirket i projektet. Kursisterne er ble-

vet interviewet og har deltaget i specifik undervisningsmetodik og didak-tik, og de har været med til at prøve både eksisterende og nyudvikledeundervisningsmaterialer og opgavetyper. Det bliver understreget, at dy-skalkuli ikke kan ”helbredes”. Det handler om, at den enkelte skal lærestrategier og særlige teknikker til at leve med funktionsnedsættelsen dy-skalkuli og håndtere tallene snarere end ”bare” tillægges mere tid, træningeller specialundervisning. Strategier og teknikker kan fx være at ”tænkehøjt” eller italesætte strategier, mens man regner eller at høre på, at andrei klassen gennemgå processen i et regnestykke trin for trin. Det kan ogsåvære at forenkle tallene, fx fjerne decimaler. Selv med en særlig indsatskommer den enkelte måske alligevel aldrig til at beherske basale matema-tiske færdigheder (CSV, 2010; Grynberg, 2010).I 2003 igangsatte den engelske regering en national strategi, somskulle fokusere specielt på børn med forringet talfornemmelse. Tiltagetbetød, at børn med specifikke regnevanskeligheder skulle diagnosticeresog samtidig modtage mere individuel støtte gennem flere visuelle, verbaleog fysiske aktiviteter. Den britiske uddannelsesekspert Jean Gross (2007)har set på evalueringer af den engelske regerings tiltag National Numera-cy Strategy (NNS). Med det formål at mindske kløften mellem dygtige ogmindre dygtige elever blev NNS igangsat i 1999. Formen var blandt an-det, at lærerne blev opfordret til at udvikle interaktiv læring for hele klas-sen fulgt op med gruppearbejde i differentierede hold, hvilket skulle er-statte den tidligere undervisningsform med selvstændigt arbejde. Medden nye form skulle børn med regnevanskeligheder lære fra de andre ele-ver frem for at sidde for sig selv. På den måde skulle den nye form ogsålægge op til et større fokus på mundtligt arbejde.Evalueringer af NNS viser dog, at fortolkningen og implemente-ring af strategien ikke er forløbet efter hensigten. Blandt andet påvisteflere forskere, at den mundtlige klasseundervisning kunne medføre øgetangst hos elever med matematikvanskeligheder. Anden forskning frem-drog, at elever med vanskeligheder, som havde fået tildelt en hjælpelærer,ikke gjorde større fremskrift end elever, som ikke fik ekstra hjælp. Hertilpåpeger Gross dog, at helt tredje forskning viste et positivt resultat,hvorfor hun pointerer, at meget af evalueringen af NNS er modstridende.Til evaluering af materialet meldte 27 skoler sig, og den overordnedevurdering var en tilfredshed med de nye metoder. Skolerne rapporteredeom flere børn med højnet selvværd og mere aktiv deltagelse. Evaluerin-

gen af tiltaget er dog kun baseret på kvalitative tilkendelser, idet de kvan-titative resultater stadig afventes.Ifølge Lundberg og Sterners (2009) bør den specialpædagogiskeindsats i førskolen og skolen foregå på organisations-, gruppe- og indi-vidniveau. Speciallærere, specialpædagogers og læreres kompetencerfremstår som meget betydningsfulde, og det samme gør samarbejdetmed forældre og elever samt mellem klasseundervisning og specialunder-visning. Ifølge Lundberg og Sterner opfordrer både forskning og praksistil, at undervisningen foregår med tydelige instruktioner fra lærerne, akti-viteter, hvor eleverne kan få sat ord på deres handlinger, anvendelse afforskellige udtryksformer og deltagelse i matematiske situationer. Lund-berg & Sterner pointerer yderligere, at nyligt publicerede studier fra Eng-land viser, at klasseundervisning kombineret med en-til-en-undervisning,giver rigtig gode resultater for elever med regnevanskeligheder, særligtnår det gælder grundskolens yngre elever. De fremhæver endvidere, atden mentale tallinje er en kritisk faktor, når det gælder dårligt udvikledetalbegreber, og at den bør have særlig opmærksomhed, når det gælderbørn med regnevanskeligheder. Da forskning generelt indikerer, at der erfor lidt undervisning koblet til tallinjen, kan dette være et område, sommatematiklærere i grundskolen bør udvikle. Lundberg & Sterner frem-hæver Griffins model, der viser, at tidlig talforståelse omhandler barnetsevne til at forstå og betjene kvantiteter og konstruere et rigt netværk afrelationer mellem tre matematiske verdener: en verden af fast mængde,en verden af tal og en verden af formelle symboler.Ifølge Lunde (2006, 2008b) er der fortsat kun lidt viden om,hvorvidt specialpædagogisk støtte afhjælper børns regnevanskeligheder.Dog er det vigtigt, at lærerne både støtter og styrker elevernes stærke ogsvage sider. Det er ifølge Lunde ikke et enten eller, men et både og.62I forhold til specialundervisning i skolen fremhæver Magne(2000) fire elementer, som er særligt væsentlige:

Opdagende indlæring.Her skal eleven selv søge viden og gerne i denforbindelse opdage, udforske og anvende det matematiske sprog. Eteksempel kan være inddragelse af konkret materiale, fx et A4-ark,hvor eleven udforsker og udfordrer sin forståelse gennem forskelligeøvelser, hvor papiret foldes på forskellige ledder.Prototype-indlæring.Metoden forudsætter, at træningstyper er af for-skellig vigtighed. Visse stofelementer er centrale, mere repræsentati-ve og derfor typiske for et givet stofområde. Læreren skal vælge pro-totyper, der vil lede barnet til at opdage vigtige matematiske struktu-rer. Læreren kan fx undervise elevernes talforståelse med tallene 0, 1,2, 3, 4, 5. Lige pludselig kan læreren overraske eleverne med tallet 34.Umiddelbart virker det som noget af et spring, men eleverne kanfaktisk herigennem opleve, at en 3’er lige pludselig er næsten ti gan-ge større end en 4’er.Produktiv træning.Magne tror ikke på mekanisk træning ved brug aftrinmetoden. En sådan tilgang passiverer eleverne. I stedet skal deopfordres til at tænke selvstændigt og reflekterende.

Magne pointerer, at den rigtige læring handler om at organisere læringenmed tanke på elevens personlige baggrund og den enkeltes læringsstil. Idag er der meget tale om problemorienteret uddannelse, åben læringsamt autonom indlæring. Alle læringsformer lægger vægt på, at eleven harmere kontrol over sin egen undervisning, hvilket Magne anbefaler.Adler (2007) fremhæver konkrete forslag til kognitiv træning ret-tet mod dyskalkuli. Han fremhæver: 1) træning af skema for tal ved atudarbejde en tallinje med brøker; 2) træning af arbejdshukommelse vedat udregne tværsum af otte-cifrede tal; 3) træning af spatiale kompetencervia opgaver med konkret materialer, fx cuisenaire-stænger63; 4) træning aftidsopfattelse, hvor der anvendes et analogt og digital ur eller via prakti-ske opgaver med tidstagning; 5)træning af arbejdshukommelse, opmærk-somhed og koncentration ved hjælp af spil, såsom skak, mastermind,bridge, canasta og sudoku.Derudover har han i forlængelse af sin matematikscreening ud-arbejdet en idébog til den videre træning og planlægning af øvelser, som63. Centicubes eller cuisenaire-stænger er et læringsværktøj, der består af små firkantede klodser iforskellige farver, som kan klikkes sammen og skilles ad igen (lidt som legoklodser). Formen erdirekte knyttet til læringsindholdet, da centicubes-værdier alle kommer til udtryk gennem klod-sernes fysiske form. Derudover har klodsen ingen overflødig funktion, som kan vildlede bruge-ren.

skal bygge på resultaterne fra screeningen. Idébogen indeholder øvelserfra ti delområder, der hver indeholder emner (kognitive processer), derifølge Lunde har betydning for arbejdet med matematik: 1) tal og cifre, 2)talbegrebet, 3) antalsopfattelse, 4) skema for tal, 5) arbejdshukommelseog opmærksomhed, 6) perception, 7) spatial tænkning, 8) planlægnings-evne, 9) tidsopfattelse og 10) logik og problemløsning.Hannell (2013) og Butterworth (2004) lægger først og fremmestvægt på talfornemmelse. Forfatterne er især optaget af træning, der kanøge tal- og mængdeforståelse såsom de øvelser, der indgår i Butterworthsscreening.64Butterworth (2003) fremhæver yderligere, at elever med dys-kalkuli ofte vil have mange nederlag bag sig og derfor også kan døje medandre vanskeligheder. Det kan fx være angst eller fortvivlelse. Han poin-terer, at det først og fremmest er vigtigt at reducere eventuel angst ogfortvivlelse hos elever med dyskalkuli.I litteraturen fremgår det, at undervisningsformen og indholdetspiller en central rolle. Her er den gennemgående anbefaling, at under-visningsformen omfatter alle tre niveauer: klasse-, gruppe- og individ-niveau. Dertil er det gennemgående, at undervisningen indeholder ele-menter, der træner de kognitive processer. Særligt for dyskalkulikere bli-ver der dels lagt vægt på øvelser, der styrker talfornemmelsen (tal- ogmængdeforståelse), dels bliver der lagt vægt på, at eleven lærer kompen-serende strategier. Træning kan foregå via spil, hvor eleven har mulighedfor selvtræning. Redskaber kan fx bestå af en almindelig eller særliglommeregner. I det følgende afsnit skal vi se nærmere på spil og redska-ber, der kan styrke talfornemmelsen samt på redskaber, der kan virkekompenserende.Hjælperedskaber

Der findes rigtig mange materialer til selvstudier, men materialerne erikke blevet grundigt evalueret. Det betyder, at det er uklart, hvor effekti-ve materialerne er, og om de virker for alle børn med dyskalkuli (Butter-worth, 2003).Butterworth (2003) anbefaler, at elev, forældre og lærere søgerstrategier uden om vanskelighederne snarere end at konfrontere demdirekte. Han anvender en analogi til farveblindhed. Ingen kendte regimervil gøre det muligt for en person, der er farveblindhed at skelne mellemrød og grøn. Imidlertid kræver strukturen i samfundet, at du stopper forrødt lys og går ved grønt lys. Det betyder, at en person, som er farve-blind, må lære andre strategier til at vurdere, hvad der er henholdsvisrødt og grønt. I forhold til dyskalkuli anbefaler Butterworth, at elevenlærer at bruge en lommeregner. Det vil kræve, at eleven forstår en givenopgave, men ikke regnefærdigheder. Han påpeger, at selv personer medsvær dyskalkuli kan have succesoplevelser med mere abstrakte aspekteraf matematik, såsom algebra, hvilket kan hjælpes på vej ved at anvendelommeregnere.En af de danske eksperter erfarer ligeledes, at elever, der ikkekan lægge selv små tal sammen, sagtens kan lære at differentiere og inte-grere og stadig forstå mere avanceret matematik. Her lader elevernelommeregnere gøre de ting, de ikke selv kan.Orton-Flynn & Richards (2000) har undersøgt potentialet for atbruge speciallommeregneren Multimedia Interactive Calculator (MIC) tilelever med matematikvanskeligheder i undervisningen. MIC operererbåde med den konkrete fase, hvor eleven skal lære tal og den mere ab-

strakte fase, hvor eleven skal anvende symboler. Orton-Flynn & Ri-chards har særligt fokus på dyslektikere (ordblinde), men MIC anvendesogså af børn med matematikvanskeligheder og børn uden vanskeligheder.Forfatterne arbejder ud fra det perspektiv, at de fleste læringsprocessergår fra læring af konkrete koncepter til forståelse af mere abstrakte kon-cepter, her matematiske symboler.Ifølge forfatterne skal eleven igennem fire stadier, når hun/hanskal lære matematik: 1) erfaring med fysisk og konkret materiale, 2) ver-balt sprog til at beskrive erfaringen, 3) billeder, der repræsenterer erfarin-gen, og 4) endelig skrevne symboler, der generaliserer erfaringen. Detførste stadie kan fx indeholde undervisningsmateriale med Cuisenaire-stænger og hverdagsobjekter, hvorigennem indskolingseleverne skal læretal, addition, subtraktion, ordenstal og kardinaltal. Ved fjerde stadie skaleleverne introduceres til mere abstrakte koncepter ved at relatere dekonkrete materialer til symboler. Sådanne symboler læres bedst ved, ateleverne lærer at tegne symbolerne og associere dem med det korrektetalord. I dette stadie bliver læsning og skrivning af tal således sammen-koblet med tælling af objekter. Orton-Flynn & Richards studie viste, atmange af eleverne var begejstrede for at bruge lommeregneren. De dyg-tige elever blev stimuleret til mere læring, og de svagere elever forekommere selvsikre.Malmer (2001) fremhæver ligeledes, at opgaveløsning ved hjælpaf konkrete materialer kan være en stor hjælp for eleverne. Her foreslårMalmer, at læreren i højere grad kan gøre brug af konkrete materialer,såsom Cuisenaire-stænger. Malmer beskriver stængerne som et relati-onsmateriale og pointerer, at de kan anvendes som et visuelt hjælpemid-del for at illustrere helheden og delene, tal i brøkform, tal i procentformm.m. Ifølge Malmer skaber de visuelle modeller et indre billedarkiv, somkan hjælpe elevens logiske tænkning. Malmer har hertil også udviklet etcomputerspil til de lidt ældre elever. Spillet indeholder tilsvarende (dogmere komplicerede) øvelser med farvede stænger, men i og med at detforegår ved en computer, undgår man, at eleverne finder arbejdet medstængerne for barnligt.Pind & Bjerre har udviklet it-hjælpemidlet Dyscalculator, som eren lommeregner-app til smartphone, der er beregnet til personer medmassive matematikvanskeligheder, herunder personer med dyskalkuli.Dyscalculator hjælper med at forstå tal og vælge regneoperationer.6565. I 2012 vandt Dyscalculatoren til Danish App Awards i kategorien ”Science og Education”.

Malmer (2001) kritiserer imidlertid den øgede brug af lomme-regnere. Ikke fordi eleverne skal tvinges til at regne alt i hovedet, menfordi det ifølge hende forhindrer eleverne i at udvikle alternative strategi-er og tankeformer.Britiske speciallærere med erfaring på området lægger vægt på atgøre tal meningsfulde gennem undervisning baseret på målsætninger,barnets handlinger og informativ feedback på barnets handlinger. Netopfeedbacken skulle motivere barnet. Når barnet modtager informativfeedback, giver det muligheder for at regne ud, hvordan en handling kanjusteres for at nå et mål. Eleven er således ikke afhængig af, at lærerenguider ham eller hende. Mere konkret anvender speciallærerne ofte leg ogspil med fysiske tal og objekter for at give eleven en forståelse af tal. Me-toderne bør håndteres af særligt uddannede lærere, som kun arbejdermed en eller få elever ad gangen (Butterworth m.fl., 2011). Butterworthm.fl. (2011) foreslår derfor øget brug af spilsoftware, som er tilpassetvanskeligheder, der opleves ved dyskalkuli, og som er målrettet talfor-nemmelsessystemetiisselapperne,fx”NumberRace”ler ”Graphogam-Maths”.Torkel Klingberg (2011) har vist en sammenhæng mellem godarbejdshukommelse og gode læsere og gode regnere. Ifølge Klingbergbelaster automatiseringsvanskeligheder desuden arbejdshukommelsen.Halvdelen af elever med indlæringsvanskeligheder har vanskelighedermed hurtig genkendelse. Han fremhæver, at elever med god arbejdshu-kommelse sædvanligvis regner hurtigt, og derfor bør arbejdshukommel-sen trænes og belastes, men ikke overbelastes. (Klingberg, 2011). Adlerhenviser blandt andet til programmerne eller spillene Lumosity66, Ro-boMemo, CogMed samt Brain Challenge fra Big Fish Games.Emerson House anvender ligeledes computerprogrammer oghar desuden fokus på en struktureret, multi-sensorisk læringstilgang(Emerson & Babtie, 2010).Et treårigt projekt startet i 2012 af Region Nordjylland og delta-gende skoler har et overordnet formål om at udbrede og styrke indsatsenover for unge med svære matematikvanskeligheder (læs mere om projek-tet i kapitel 4). Allerede nu har projektet kunnet hjælpe deltagende eleveri eksamenssituationer med flere hjælpemidler og forlænget forberedelses-tid. Der er endnu ikke en særlig løsning for elever med ren dyskalkuli,men de har haft gode erfaringer med computerspil. I projektet har de66. Se fx www.lumosity.com.

søgt at finde computerløsninger med henblik på at anvende leg somhjælpemetode snarere end træningsopgaver. Spillet ”Brain Challenge” erforeløbig blevet anvendt, hvor eleverne skal spille mindst 20 minutterhver dag. Brain Challenge arbejder med tal og talbegrebet, antalsopfattel-se, skemaer for tal, arbejdshukommelse, opmærksomhed, planlægnings-evne, logik, problemløsning og spatial tænkning, hvor spillet bidragermed tydelig visuel struktur. Spillet findes i forskellige versioner, så der ermulighed for at graduere efter elevens behov og evne. Dertil får elevernepå baggrund af testresultaterne specielt tilrettelagte forløb, der passer tilden enkelte elevs behov og udvikling.Et par danske eksperter, som har arbejdet med spillet Brain Cha-llenge, udtaler, at de har gode erfaringer med spillet. Deres erfaring er, atspillet øger opmærksomheden, reaktionsevnen og hukommelsen. Imid-lertid bliver det også pointeret, at det ikke er alle, der bliver ved med atsynes, at spillet er sjovt.

Vi er imidlertid ikke stødt på evalueringer af støtteformer, som lever optil nogen form for evidenskrav. Forudsat at der foregår en testning afelever, som kan identificere elever med dyskalkuli, vil det være en relativenkel sag at foretage en evaluering af disse på højt evidensniveau. Hvisstøtten sættes ind over for den enkelte elev, kan eleverne fordeles påstøtteformer ved lodtrækning. Hvis støtten sættes ind over for en klasse,kan klasserne fordeles på støtteformer ved lodtrækning. I begge tilfældevil det være muligt at leve op til kravene til et RCT-forsøg.67

FORSKNING OG EKSPERTERDette kapitel giver et overblik over eksperter og netværk i Danmark,Sverige, Norge og Storbritannien samt enkelte eksperter uden for denævnte områder, hvor vi lægger vægt på de mest fremtrædende på feltet.Sidstnævnte eksperter har vi fået anbefalet af de danske eksperter, vi lø-bende har haft kontakt til.De personer, der her er fremhævet, har det til fælles, at de allearbejder med dyskalkuli i et større omfang. Flere af ressourcepersonerneanvender og arbejder dog ud fra bredere begreber og definitioner, så-som ”matematikvanskeligheder” eller ”regnehuller”, hvor dyskalkuli kuner en snæver underkategori.68Under personbeskrivelserne er der stor forskel på mængden afindhold. Det skyldes for det første forskelle i, hvilken og hvor megeninformation der er tilgængelig om hver enkelt person i forbindelse mednavnesøgninger på internettet. For det andet er der forskel på, hvad hverenkelt person har bidraget med af oplysninger om sig selv og i givet fald ihvilket omfang. Vi skal pointere, at den rækkefølge, personerne optræderi, er helt tilfældig. Som nævnt i kapitel 2 har vi i litteraturlisten inddragetal den litteratur, vi har fundet relevant – også den litteratur, vi ikke harhenvist til i løbet af kortlægningen. Området er meget holdningspræget,

Dyskalkuli er et meget uudforsket område generelt, men særligt i Dan-mark findes der stort set ingen forskning på området.Center for Specialundervisning for Voksne (CSV) SydØstfyn an-fører, at der i Danmark stort set ikke er foretaget videnskabelige under-søgelser af dyskalkuli (CSV, 2010). CSV igangsatte i 2010 et udviklings-projekt om dyskalkuli, hvor målet var at afprøve og udvikle undervis-ningsmetoder og -materialer. Arbejdsgruppen bestod af førende eksper-ter på området.CSV-projektet tager for det første udgangspunkt i en fælles er-kendelse af, at der er en gruppe borgere med specifikke matematikvan-skeligheder, som ikke får tilstrækkeligt udbytte i de etablerede tilbud in-den for forberedende voksenundervisning (FVU-matematik) og special-undervisning for voksne. For det andet tager CSV-projektet udgangs-punkt i tesen om, at der mangler videnskabelig forskning på området. Pågrundlag af projektet konkluderer ekspertgruppen, at der ikke er foreta-get videnskabelige undersøgelser på området i Danmark.I forlængelse af ovenstående projekt blev der igangsat andreforskningsbaserede undervisningsforsøg, dog er der fortsat bemærkelses-værdigt lidt forskning på området.Flere af de eksperter, som vi har været i kontakt med, anfører, atder i Danmark ikke findes ”rigtig” forskning om dyskalkuli. Argumenteter blandt andet, at størstedelen af de undersøgelser der findes er megeterfaringsbaserede og befinder sig på kanten af reel forskning. Derudoverer de fleste af de undersøgelser, der er foretaget i Danmark, centreretomkring den samme, mindre gruppe af eksperter på området. De mestfremtrædende eksperter vil vi beskrive i det følgende afsnit.EKSPERTER I DANMARKLENA LINDENSKOV

matematik og samfundsfag og er ph.d. med speciale i matematikunder-visning. Lindenskovs fokusområder er pædagogik, læring og filosofi samtdidaktik og uddannelse, herunder matematikkens didaktik, matematik-vanskeligheder og kompetenceteori. Særligt lægger hun vægt på relevansaf matematiklæring og på børn, unge og voksne, der har vanskelighedermed at lære matematik. Aktuelt er hun sammen med Peter Weng ved atudarbejde en dansk model for tidlig indsats i matematikundervisning.69Lindenskov har været involveret i flere projekter vedrørende ma-tematikvanskeligheder og talblindhed blandt andet CSV-projektet, somer beskrevet først i dette kapitel. Hun mener klart, at anerkendelsen afproblemet har betydning, idet der kan være mange følelser forbundetmed at have problemer med tal. Hun påpeger, at tal, diagrammer ogplanlægning af tid er meget styrende for vores hverdagsliv, og det erhendes erfaring, at mange har oplevet, at de på grund af deres vanske-ligheder med at lære matematik er blevet regnet for at være dumme.Inspireret af Oluf Magne og Olav Lunde argumenterer Linden-skov for anvendelsen af begrebet ”regnehuller” på sammen måde somblandt andre Peter Weng (Böttger m.fl., 2013; Lindenskov, 2005; Lin-denskov & Weng, 2005). Argumentet er, at ”regnehuller” er et didaktiskbegreb med et dobbeltindhold. Ideen er at tage udgangspunkt i de ma-tematiske vanskeligheder, eleven møder, snarere end at tage udgangs-punkt i eleven. Det vil sige, at begrebet omhandler de vanskeligheder(regnehuller), som alle elever kan opleve før eller siden70. Sammen medPeter Weng argumenterer Lindenskov endvidere for, at der er brug foren helhedsvurdering af den enkelte elev (Lindenskov & Weng, 2005) (semere i forbindelse med omtalen af Peter Weng senere i dette kapitel).Lindenskov har gennemført flere projekter vedrørende special-undervisning, fx ”Matematik i specialundervisningen” (2011). Hun pro-blematiserer blandt andet, at lærere og forskere især koncentrerer sig ombørnenes personlige og sociale kompetencer i specialundervisningen,snarere end at betragte de sociale og personlige kompetencer som noget,der spiller sammen med de faglige kompetencer. Det bliver fx problema-tisk, når lærerne vurderer, at børn ikke er skoleparate på baggrund af de-res sociale og personlige kompetencer, idet børnene bliver frataget deresmuligheder for faglig læring. Dertil fremhæver Lindenskov også, at det er

problematisk for både elever og lærere, hvis børnene vender tilbage tilnormalklassen uden at have lært ret meget matematik.Vanskeligheder ved matematik kan afhjælpes i langt højere grad,end de bliver i dag ved at bygge en bro over de såkaldte ”regnehuller”.Med inspiration fra Oluf Magne mener hun, at der skal mere fokus påundervisningsdifferentiering, så matematikundervisning bliver ”individu-el livsmatematik”, og alle elever får den støtte, de har brug for. Herunderser hun et behov for, at læreuddannelsen forbedres, så matematiklærerebliver bedre til at observere og arbejde med elevers matematikproblemer.Dette kan blandt andet ske ved at anvende test og samtaler for at klar-lægge elevernes individuelle vanskeligheder.PETER WENG

Peter Weng er lektor på Institut for Skole og Læring på Professionshøj-skolen Metropol. Han arbejder på det fagdidaktiske område og har imange år arbejdet indgående med elevers matematikvanskeligheder.Hans fokusområder er elevers vanskeligheder ved læring af matematik,problembehandling som redskab i og mål for matematikundervisningensamt evaluering.Aktuelt er Weng, sammen med Lena Lindenskov ved at udar-bejde en dansk model for tidlig indsats i matematikundervisning.71Fornylig har Weng blandt andet også udgivet bogenHåndbog i matematik igrundskolen(2013) sammen med Michael Wahl Andersen. Bogen beskæf-tiger sig med nuancerede og aktuelle problemstillinger af betydning formatematikfaget og matematik-didaktikken.Weng har desuden været med til at udarbejde et projekt om tid-lig matematikindsats til marginalgrupper. Projektets overordnede mål erat fremme og kvalificere samarbejdet i den personkreds, der bliver ind-draget, når elever er i matematikvanskeligheder. Projektet skal støtte ele-ver med matematikvanskeligheder og de elever, der kan være på vej ud ivanskeligheder. I projektet vurderes eleverne ikke på deres karakterer,men på MG-prøver (Matematik Grundlæggende), som er et system,Weng har udarbejdet. Ideen er, at karakterer ikke skal spille en hovedrol-le, men at det personlige, holdninger og forståelse kommer mere i fokus.Foreløbige analyser viser, at eleverne rykker sig i en positiv retning.Weng argumenterer på samme måde som blandt andre Linden-skov for anvendelsen af begrebet ”regnehuller” (Böttger m.fl., 2013;71. Se mere om denne i kapitel 4.

Lindenskov & Weng, 2005; Weng, 2011). Argumentet er, at ”regnehuller”er mere anvendeligt i det praktiske arbejde (se under Lena Lindenskov).Sammen med Lena Lindenskov argumenterer Weng endvidere for, at derer brug for en helhedsvurdering af den enkelte elev, og at der på nuvæ-rende tidspunkt ikke findes en test, der er anvendelig i forhold til dettehelhedssyn. De mener ikke, at de test, der anvendes i dag, inddrager til-strækkelig mange aspekter, ligesom lærerne ikke har nok redskaber til atvurdere den enkelte elev, når der opstår vanskeligheder (Lindenskov &Weng, 2005).MICHAEL WAHL ANDERSEN

Michael Wahl Andersen (cand.pæd.psyk.) er lektor ved Professionshøj-skolen UCC. Andersen har fokus på pædagogik, undervisning, uddannel-se. Han er i øvrigt tilknyttet Videnscenter for Specialpædagogik.Andersen fokuserer på sproget og ser sproget som afgørende forelevernes mulighed for at lære matematik. Ifølge Andersen fastholdeseleverne på deres aktuelle udviklingsniveau, hvis ikke de har de sprogligeforudsætninger, der skal til for at forstå matematikundervisningen,Andersen har blandt andet været med til at igangsætte et toårigtudviklingsprojekt, ”Sæt billeder på matematikken”, i samarbejde medOrdblindeinstituttet i Ballerup. Projektet har blandt andet fokus på ar-bejdshukommelsens funktion i forbindelse med læring i matematik. Ud-gangspunktet er, at matematik er et meget abstrakt fag, hvilket kan skabevanskeligheder for nogle børn. I projektet bliver der arbejdet med atkoble flere ord og billeder til den faglige læsning for at illustrere matema-tikken. Når der bliver sat flere mentale billeder på matematikken, bliverdet nemmere for eleverne at forstå matematik, hvis de kan associere be-greberne med mentale billeder.Projektet tager udgangspunkt i hjerneforskning, herunder hu-kommelsesforskning, hvormed Andersen argumenterer for, at elevernesarbejdshukommelse må aktiveres, før viden sætter sig fast, fx ved hjælpaf billeder og sprog. Derefter bliver det faktuelle lagret i langtidshukom-melse ved indlæring og repetition (Andersen, 2011). Andersen søger så-ledes at åbne op for vigtigheden af sammenhængen mellem hjernen, læ-ring og didaktik.Andersen arbejder grundlæggende med elever med matematik-vanskeligheder. Han problematiserer, at der er mange, som stort set udenempirisk baggrund og uden en klar definition diagnosticerer mennesker

til at have dyskalkuli. Andersen anser dyskalkuli som synonymt med ellersamlebetegnelse for en række forhold. Han påpeger, at der generelt erenighed om, at mennesker med såkaldt dyskalkuli har svært ved at læreog huske aritmetiske fakta og at udføre regneprocedurer. Som han serdet, kan det komme til udtryk på mange forskellige måder; Personer meddyskalkuli har svært ved at vurdere, om de har penge nok, når de er udeat handle – de har svært ved at tælle penge op, betale for varer og få pen-ge retur. De har også svært ved at lære klokken, overskue køreplaner ogbetale for busbilletten. De kan ligeledes have vanskeligt ved at lave madefter en opskrift mv. Dyskalkuli har også stor indflydelse på personersuddannelsesmuligheder. Samtidig understreger Andersen, at dyskalkuliikke er et entydigt begreb, og at der blandt forskere er forskellige hold-ninger til, hvad begrebet dækker.PERNILLE PIND (OG ERIK BJERRE)

Pernille Pind er konsulent inden for området matematik og matematik-vanskeligheder. Hun efteruddanner folkeskolelærere og afholder og ud-byder kurser alt sammen primært om matematik og oftest også matema-tikvanskeligheder. Derudover driver hun og hendes mand, Erik Bjerre,firmaet ”Pind og Bjerre”. De skriver og udgiver begge bøger samt udvik-ler it-læringsmidler og -hjælpemidler.Pind og Bjerre har blandt andet udviklet it-hjælpemidlet Dyscal-culator, som er en lommeregner-app til smartphone beregnet til personermed massive matematikvanskeligheder, herunder personer med talblind-hed, som kan hjælpes til at forstå tal og vælge regneoperationer.Pernille Pind laver derudover udredninger af børn, unge ogvoksne i matematikvanskeligheder for Institut for Kommunikation ogHandicap i Århus. Gennem de sidste fem år har Pind afholdt såkaldteTaltrygforløb: en kombineret indsats for elever med matematikvanske-ligheder og et efteruddannelsesforløb for undervisere inden for områdetmatematikvanskeligheder. Standardforløbet er 10 uger med to timerugentligt for ni elever og tre lærere, hvoraf de to lærere er faste gennemforløbet, og pladsen til den tredje lærer går på omgang blandt skolensøvrige matematiklærere. Forløbene tilrettelægges dog efter skolens øn-sker.Pind mener, at årsager til matematikvanskeligheder groft kanopdeles i tre typer; 1) problemer med tal, 2) problemer med sprog og 3)manglende hverdagserfaringer. Herefter vil Pind kun kategorisere den

første som talblindhed. Pinds erfaring er også, at årsagerne ofte kommeri kombinationer. Med hensyn til årsager til talproblemer læner Pind sigforskningsmæssigt op ad den britiske professor Brian Butterworth ogStanislas Dehaene. Pind mener, at det giver mening at tænke i, at menne-sker er født med to evner for tal. Den ene er evnen til at registrere småantal uden at tælle, og den anden er evnen til at skønne forskel på mæng-der med forskellige antal.Med inspiration fra Snorre Ostad mener Pind, at problemer medtal ofte kommer til udtryk i den enkeltes strategier for at regne med småtal, hvor de ofte vælger at tælle i stedet for at regne. Pind oplever også, atsproget har betydning, og at særligt oversættelsen mellem tekstopgave ogregnestykket til at løse tekstopgaven volder vanskeligheder. Her lænerhun sig op ad Gudrun Malmer. Hverdagserfaringernes betydning for ma-tematikforståelsen kommer fx til udtryk gennem manglende fornemmel-se for afstande, vægt, priser mm. (her er hun inspireret af bl.a. Olav Lun-de og Oluf Magne).Når Pind selv laver udredninger, anvender hun sit eget testmate-riale og sine egne interviewspørgsmål. Hun har hentet inspiration til sittestmateriale fra mange forskellige test, heriblandt dem hos Brian But-terworth, Björn Adler, Snorre Ostad og Gudrun Malmer. Derudover harPind hentet inspiration fra FVU (Forberedende Voksenundervisning),som har større fokus på det virkelighedsnære. Målet for Pind er at laveen nuanceret beskrivelse af en persons matematikkompetencer og kom-me med forslag til efterfølgende indsats og eventuelle kompenserendestrategier for både personen selv og dennes uddannelsesinstitution ellerarbejdsplads.Yderligere er Pind i gang med at udvikle og afprøve materiale tiltest af børn i 0. til 2. klasse med tilhørende undervisningsmateriale,hvormed forældre og/eller lærere kan give barnet målrettet ekstra støtte.Pind er derudover medlem af matematikekspertgruppen (ek-spertgruppen for styrket undervisning i matematik), som blev nedsat in-den skolereformen (ultimo 2012).BENT LINDHARDT

(Dansk Special Matematik) og har været foreningens formand lige siden.Foreningen dækker et bredt udvalg af professioner og har omkring 80medlemmer. Lindhardt sidder derudover i den nordiske komite forNORSMA (The Nordic Research Network on Special Needs Educationin Mathematics).Bent Lindhardt har tidligere som lærer arbejdet med at udviklenyt indhold og nye organisationsformer inden for specialundervisning imatematik. Aktuelt underviser han blandt andet på Pædagogiske Di-plomuddannelser (PD-moduler) omkring matematikvanskeligheder.Desuden er Lindhardt i gang med at forberede en bog for DAFOLO ommatematikvanskeligheder.I kraft af sin viden om emnet er Lindhardt en hyppig foredrags-holder i Danmark, og han har afholdt adskillelige kurser og konferencerom spørgsmål og problemstillinger om elever med vanskeligheder gen-nem de seneste 30 år. Han har derudover bidraget med flere artikler omemnet til fagblade og har gennem flere år været forfatter/medforfattereller redaktør på mange matematikbøger til folkeskolen – omkring 200titler.Gennem sit virke i Nationalt Videnscenter for Matematikdidak-tik i perioden 2007-2011 har Lindhardt været involveret i flere udvik-lingsarbejder om matematikvanskeligheder, herunder vedrørende elevermed specifikke vanskeligheder. Lindhardt har yderligere gennem en år-række haft kontakt til en del forældre og elever/unge, som har ønsket atvide mere om egne vanskeligheder i matematik.Lindhardt er derudover medlem af matematikekspertgruppen(ekspertgruppe for styrket undervisning i matematik), som blev nedsatinden skolereformen (ultimo 2012).LENE ØSTERGAARD JOHANSEN

til FVU-lærer. Afhandlingen bevæger sig i grænselandet mellem matema-tik didaktik, almen didaktik og sociologi.Johansen har i 1990’erne undervist i blandt andet matematik påhtx. Derefter har hun arbejdet med didaktik, pædagogik og psykologisom lektor og konsulent ved Danmarks Erhvervspædagogiske Lærerud-dannelse. Fra 2000 har hun været ansat på Aalborg Universitet først somph.d.-studerende og efterfølgende som studielektor med forskningsretved Adgangskursus, hvor hun underviser håndværkere i matematik fra 0-til A-niveau. I forbindelsen med udviklingen af FVU-matematik blev in-teressen for matematikvanskeligheder født, og Johansen var med iNORSMA fra begyndelsen i 2002 og har skrevet flere generelle artiklerom emnet og holdt en række oplæg især inden for voksenuddannelses-verdenen.De senere år har Johansen haft fokus på betydningen af sprog imatematikundervisningen, både det talte og det skrevne, og har blandtandet haft fokus på overgangen fra folkeskolen til de gymnasiale uddan-nelser og faglig læsning og skrivning i matematik i gymnasiet. Johansenlæner sig op ad norsk forskning, som viser, at der er en sammenhængmellem vanskeligheder ved at tilegne sig sprog og at tilegne sig matema-tikfærdigheder, da matematik indeholder mange nye ord og begreber,som kan volde vanskeligheder for elever, der har svært ved sprog. IfølgeJohansen er der derfor brug for, at lærerene fokuserer på den sprogligebevidsthed for at skabe en inkluderende og matematikvanskelighedsfo-rebyggende undervisning, der kan rumme børn med forskellige baggrun-de, såvel danske etniske børn som børn med anden etnisk baggrund.Fra 2008 har Johansen indgået i OECD’s numeracyekspertpanelfor den nye undersøgelse af voksnes kompetencer, PIAAC. I forbindelsemed dette arbejde har hun været involveret i udviklingen af testen ivoksnes regnefærdigheder. Johansen har ligeledes været en af ressource-personerne for gruppen hos SFI – Det Nationale Forskningscenter forVelfærd, der har gennemført den danske del af undersøgelsen.Johansen interesserer sig hovedsagligt for den del af matematik-vanskeligheder, som bliver tydelig i klasseværelserne, og for hvorledeshun kan være med til at uddanne lærerne, så de bliver bedre klædt på tilat hjælpe den enkelte elev.Johansen omtaler to forskellige forståelser af matematikvanske-ligheder: en snæver forståelse og en bred forståelse. Den snævre forståel-se (dyskalkuli) dækker over den specifikke elevgruppe, der har problemer

i forhold til regnefærdigheder, men ellers er normalt repræsenteret i deandre fag. Den brede forståelse dækker derimod over alt, der har indfly-delse på elevens udbytte af undervisningen. Det vil sige, at eleverne kanhave vanskeligheder i andre fag end blot matematik. Vanskelighederne ide andre fag kan være som følge af matematikvanskelighederne eller kanhave samme årsag som disse. Johansen vedkender sig den brede forståel-se af matematikvanskeligheder.Ifølge Johansen er den nordiske litteratur omkring matematik-vanskeligheder opdelt i forskellige professionsgrupper. Professionsgrup-perne er fx neuropsykologer, skolepsykologer og specialpædagoger samtmatematiklærere og matematikdidaktikere, som har forskelligt fokus ogadresserer ansvaret for elevens matematikvanskeligheder forskellige ste-der. Neuropsykologer, skolepsykologer og specialpædagoger fokusererprimært på eleven, som bærer matematikvanskeligheden, hvorimod ma-tematiklærere og matematikdidaktikere fokuserer på undervisningen. Jo-hansen introducerer den didaktiske trekant, som illustrerer mødet mel-lem lærer, elev og fagstoffet. Når der opstår matematikvanskeligheder, erdet oplagt, at man søger kilden til vanskelighederne hos en af de tre fak-torer eller i mødet mellem dem. Hun er dog også opmærksom på, at so-ciale strukturer og rolle-relationerne i klasseværelset og i skolen kan haveen væsentlig betydning.STEEN POLK

Steen Polk er pædagogisk konsulent tilknyttet PPR (Pædagogisk Psyko-logisk Rådgivning) i Svendborg, Derudover er han formand for Dan-marks Specialpædagogiske Forening.Polk er endvidere en af de fem eksperter bag CSV-projektet,som kort er beskrevet først i dette kapitel. Polks arbejde i projektet be-stod i at teste børn og unge med forskellige prøver for at afdække, omtalblindhed var deres primære vanskelighed. I alt blev vanskelighedernehos 85 børn og unge afdækket med forskelligartede test.Ifølge Polk mangler der konkret forskning på området, og stårdet til ham, skal læreseminarerne fokusere mere på specialeundervisningog lærerne have mere viden om de specifikke matematikvanskeligheder.STEEN HILLING

Karin Jessen er uddannet folkeskolelærer med linjefag i matematik. Hunhar i mange år undervist i matematik i folkeskolen. De sidste seks år harhun udelukkende undervist i FVU-matematik. Jessen er den person, derhar den direkte kontakt til kursisterne. Særligt observerer og lytter hun til,hvad de siger, og hvordan de løser de forskellige opgaverJessen var desuden en af eksperterne bag dyskalkuli-projektet påCSV SydØstfyn, hvor hun testede de voksne deltagere i projektet.I 2012-13 har Jessen været den ene lærer i forsøgsundervisnin-gen på Svendborg Erhvervsskole.HENRIK SKOVHUS

Henrik Skovhus er speciallærer og konsulent ved Nordjysk Læse og Ma-tematik Center. Han har tidligere arbejdet på Taleinstituttets, hjerneska-decenter under Region Nordjylland, hvor han beskæftigede sig med træ-ning samt afasi-undervisning72af personer med erhvervet hjerneskade.Som en del af sit arbejde på Taleinstituttet har Skovhus særligt beskæfti-get sig med udredning og undervisning af personer med (specifikke) reg-nevanskeligheder. I den forbindelse har han udviklet en computerbaserettest (LINU-test) og dertil afholdt kurser og oplæg på folkeskoler, ung-domsuddannelser, PPR-kontorer mv. omkring ”matematikvanskelighe-der”.Siden 2007 har Skovhus samarbejdet med Björn Adler omkringoversættelse, bearbejdning og salg af hans materialer i Danmark, og haner derfor fortrolig med Adlers materiale.Aktuelt er Skovhus blandt andet tilknyttet et udviklingsprojektmed titlen ”Unge med matematikvanskeligheder – dyskalkuli”, underRegion Nordjylland.

Olav Lunde er magister i pædagogik, specialist i pædagogisk-psykologiskrådgivning og tidligere leder af PP-tjenesten (dansk PPR) i Klepp. I dager han tilknyttet kompetencecentret i Kristiansand og Høgskolan i Agde.Desuden er han seniorrådgiver i Sørlandet Kompetansesenter.Lunde har udgivet flere bøger, der dækker området dyskalkuli,blandt andet bogenNår tal gi’r kaos(2012), hvor han har samlet og be-skrevet sin teoretiske og praktiske viden. Bogen indeholder en gennem-gang af kendetegn for matematikvanskeligheder, nordisk og internationalforskning, forskning i hvorfor tal ”gi’r kaos” for nogen, sammenhængmed andre vanskeligheder, prøver, test og vurdering, udredning, kort-lægning og tiltag, udformning af tiltag og motivation samt en omfangsrigopslagsbog med referencer.SNORRE OSTAD

Snorre Ostad har gennemført omfattende forskning i matematikvanske-ligheder (1999). Han har især arbejdet med teorier om informationsbear-bejdning, der knytter sig til læringsvanskeligheder. Regnevanskelighederforklares med vanskeligheder med effektive strategier til at kunne hentearitmetiske informationer (talfakta eller basisfakta). Ostad har blandt an-det påvist, at elever med regnevanskeligheder anvendte mere primitive ogfærre strategier end normalt fungerende elever, hvilket var baggrundenfor diskussionen om, hvorvidt matematikvanskeligheder er en kvalitativvanskelighed, eller om der er tale om en forsinket udvikling (Lunde,2012).ELIN REIKERÅS

Tone Dalvang er rådgiver ved Sørlandet Kompetansecenter, hvor hunarbejder i statslig specialpædagogisk tjeneste (Statped), som er en special-pædagogisk støttetjeneste for norske kommuner)Dalvang er fortaler for at bevæge forskning og praksis om ma-tematikvanskeligheder væk fra en diagnose- og specialundervisningsori-enteret tilgang mod en tilgang, der i højere grad fokuserer på eleverneslæringspotentiale og på udvikling af inkluderende undervisningsformer.Dalvang har blandt andet skrevet en artikel sammen med OlavLunde, hvor de redegør for fire forskellige forklaringsmodeller til forstå-else af læringsvanskeligheder i matematik: den medicinske/neurologiske,den psykologiske, den sociologiske og den didaktiske forklaringsmodel. Iartiklen er fokus på den didaktiske model, hvor forfatterne opstiller enmodel, der kan bruges som ”kompas” både til forståelse og afhjælpningaf specifikke læringsvanskeligheder i matematik. Modelen integrerer ele-vens læringsforudsætninger, undervisningens indhold og form og de ottematematikkompetencer fra det danske KOM-projekt.

Oluf Magne er professor og forsker i indlæringspsykologi og special-pædagogik med særligt fokus på matematik. Han omtales ofte som ”thegrand old mand” inden for forskning om matematikvanskeligheder, oghan er forfatter til en række bøger og artikler om elever med matematik-vanskeligheder.På baggrund af et studie af Magne oprettede den svenske rege-ring i 1963 ”matematikklinikker”, som skulle være et støttetilbud til ele-ver med matematikvanskeligheder73(Magne, 2004).Han har blandt andet publiceret en meget omfattende bibliografi(2001, revideret 2003), hvor han har systematiseret ca. 5.000 forsknings-73. Klinikkerne blev afskaffet igen i 1980.

dokumenter om dårlige præstationer i matematik, hvoraf de første do-kumenter er fra 1886. Denne bibliografi har sandsynligvis været en væ-sentlig årsag til, at fagdisciplinen matematikvanskeligheder så hurtigt op-nåede anerkendelse i Norden (Lunde, 2012).I 1950’erne gennemførte Magne en omfattende undersøgelse afden svenske folkeskole. På grundlag af undersøgelsen nåede han frem tilen hypotese om, at ca. 15 pct. af eleverne kunne betegnes lavt præsteren-de i matematik. Der var tale om en heterogen gruppe uden andet til fæl-les, end de klarede sig langt under niveau i matematik.Desuden var Magne den første til at rette søgelyset mod psyko-logiske og sociale faktorer som årsag til lave scorer i matematik. Han ud-gav i 1967 en lærebog om matematikvanskeligheder (Lunde, 2012).Magne søger at gøre op med det traditionelle perspektiv, hvormatematikvanskeligheder er placeret hos den enkelte elev, hvilket diag-nosen dyskalkuli er et eksempel på. Magne anvender begrebet SUM-elever (Särskilda Utbildningsbehov i Matematik) om elever med matema-tikvanskeligheder (Magne, 2001, 2004).Magne anlægger et systemisk perspektiv og mener, at undervis-ningen af såkaldte SUM-elever som udgangspunkt skal foregå i tilknyt-ning til tre aktører, der er involveret i elevens vanskeligheder: eleven selv,matematikken og det netværk, der afgør, om eleven har vanskeligheder.Magne omtaler især den specialpædagogiske tilgang. Han tagerafstand fra den klassiske tilgang, som han kritiserer for at være en passivformidlingsdidaktik. Magne påpeger, at eleverne skal være aktive, tænkepå egen hånd og samarbejde socialt. Samtidig skal den enkelte elev ud-vikles i og igennem et socialt netværk. Læreren skal derfor handle stimu-lerende og give eleverne anvisninger.Magne er fortaler for, at matematikken skal være relevant foreleven og elevens liv – det han betegner ”livsmatematik”. Livsmatematiker ifølge Magne at møde, bearbejde og beslutte problemer i hverdagen.Elevens egne hverdagserfaringer om husholdning, fritid, natur og kulturmv. skal udnyttes. Den praktiske matematik bør altid knyttes til det so-ciale liv, fx penge og indkøb, biografture, slikkøb mv.Magne gør desuden op med, at matematikregler skal læres i enbestemt rækkefølge, fx med de fire basale regnearter, hvor eleverne førstlærer addition, dernæst subtraktion, multiplikation og til sidst division.Magne omtaler i den forbindelse prototype-indlæring, hvor man fx kantænke på addition og subtraktion som modsatte regnearter, det vil sige to

Gudrun Malmer er underviser på Lärarhögskolan i Malmö. Malmer harmange års erfaringer med undervisning af elever med matematikvanske-ligheder, og hun har skrevet en lang række bøger og artikler om emnet. I1999 blev hun udnævnt til æresdoktor ved Göteborg Universitet.Malmer har udviklet ALP-testen, som er en screeningstest, derafdækker færdigheder i afkodning, læseforståelse, matematiske grundbe-greber og matematisk-logisk tænkning.Ifølge Malmer skal man ændre matematikundervisningen, så derer mindre fokus på regningen og mere fokus på logisk tænkning, mundt-lig matematik og handlingsmatematik.ARNE ENGSTRØM

Gunnar Sjöberg er forsker ved Umeå Forskningscenter for Matematikdi-daktik (UFM).Sjöberg har tidligere arbejdet som folkeskolelærer, primært sommatematik- og speciallærere i udskolingen. Senere læste han pædagogikparallelt med lærerjobbet og blev siden ansat på Institut for matematik,teknik og videnskab på Umeå Universitet i perioden 2001-2006.Aktuelt arbejder Sjöberg inden for det matematikdidaktiske om-råde med forskning på halvtid samt med undervisning på instituttet. Iden resterende tid arbejder han dels som matematiklærer, dels med råd-

givning og udviklingsarbejde med fokus på elever med særlige behov imatematik.I hans afhandlingOm det inte är dyskalkyli – vad är det då?har hananvendt interview, klasselokaleobservationer på video, spørgeskemaersamt en større database med 200 elever fra 5. klasse og op til 2. g i gym-nasiet. Sjöbergs ambition har været at formidle de erfaringer, som ele-verne har haft med folkeskolens matematikundervisning samt at give etbillede af, hvordan de mente, at undervisningen skulle have været forbedre at passe til dem.Sjöberg har i sin afhandling kritiseret begrebet ”dyskalkuli”. Af-handlingen ser på dyskalkuli fra to aspekter. Først undersøges begrebetdyskalkuli gennem litteraturen fra 1992 og frem. Dernæst følger en un-dersøgelse af elever, der lider af dyskalkuli, som forløb over en seksårigperiode med 200 elever, hvoraf 18 elever havde matematikvanskelighe-der. Undersøgelsen viste en række tvivlsomme og uklare omstændighe-der omkring begrebet dyskalkuli, herunder tvetydighed med hensyn tildiagnosticeringen af dyskalkuli. Sjöberg konkluderede, at det var nød-vendigt at anvende begrebet med forsigtighed grundet de store uklarhe-der forbundet med det. Det empiriske studie viste også, at feltet indehol-der stor kompleksitet. Eleverne angav dårligt arbejdsmiljø, store klassersamt stress og nervøsitet ved prøverne som forklaring på deres vanske-ligheder i matematik. Undersøgelsen viste endvidere, at gode og dygtigelærere var med til at nedbringe problemerne, såvel som skoleskift ogsamarbejde med andre elever også havde positiv indvirkning på elevernesfærdigheder.BJÖRN ADLER

Den svenske neuropsykolog Björn Adler har mange års erfaring meddyskalkuli. Han har skrevet flere bøger om emnet, og som et led i sit ar-bejde har han udviklet et screeningsmateriale, som kan bidrage med indi-kationer om mulige specifikke matematikvanskeligheder/dyskalkuli hosunge og voksne (læs mere om screeningsværktøjet i kapitel 4).Ifølge Björn Adler er det primære problem, når et barn har dy-skalkuli, at barnet har svært ved automatisk at udvælge information, nården behøves, fx ved udregning af matematikopgaver. Eleven kan derfornogle gange præstere rigtig godt, mens det andre gange går galt. Adlermener således, at svingende præstationer er karakteristisk for dyskalkuli-

kere. Han fastslår, at dyskalkuli kun omhandler specifikke og speciellematematikvanskeligheder og ikke al matematik.Adler fremhæver desuden elevens fiasko-oplevelser ved dele afmatematikken, som kan medføre følelse af mindreværd og angst, somkan have negativ indvirkning på elevens trivsel. Hertil anvender han be-grebet ”pseudo-dyskalkuli”, hvor det snarere drejer det sig om en tilstand,hvor eleven kan have en følelsesmæssig blokering over for faget matema-tik. I den forbindelse kritiserer Adler specialundervisning, idet den storeindsats for at afhjælpe elevens matematikvanskeligheder kan være med tilat øge elevens dårlige selvværd, idet eleven fortsat ikke kan løse regneop-gaver.Adler har som nævnt udviklet et screeningsværktøj, der kan testefor talblindhed:Matematikscreening I-II-III.Matematikscreeningen henven-der sig til henholdsvis 7-9 årige (I), 10-15 årige (II) og 16 årige og opefter(III).74INGVAR LUNDBERG

Ingvar Lundberg (1934-2012) var professor emeritus i psykologi ved Gö-teborg Universitet. Han var internationalt kendt for sin forskning i læse-og skriveudvikling samt dysleksi (ordblindhed). Lundbergs fokusområdevar læseindlæring, herunder hvad der ligger bag dysleksi, og om det kanforebygges, samt hvilke sociale, kognitive og sproglige forudsætningerder forudsætter en positiv læseudvikling. I den forbindelse har Lundbergogså interesseret sig for sammenhængen mellem læsevanskeligheder ogregnevanskeligheder.Lundberg startede som folkeskolelærer i Stockholm og blev se-nere tilknyttet Institut for psykologi (Psykologiska Institutionen) vedStockholm Universitet. Efterfølgende blev Lundberg tilknyttet UmeåUniversitet som professor i udviklingspsykologi, hvor han var frem til1995, for herefter at flytte til Göteborg Universitet.Lundberg har sammen med Katarina Herrlin udviklet et af Sve-riges to dominerende pædagogiske redskaber til identifikation af eleverslæseudvikling og -færdigheder,God läsutveckling.I 2009 blev Lundbergtildelt ”Hans Majestät Konungens medalj i åttonde storleken” for sinindsats i forbindelse med læseforskning og dysleksi.Inden for området dyskalkuli har Lundberg primært publiceretsammen med Görel Sterner. De har blandt andet udarbejdet rapporten74. Se mere om screeningen i kapitel 4.

Dysklakuli – finns det? – Aktuell forskning om svårigheter att förstå och användetal(2009), en forskningsoversigt om børns regnevanskeligheder. Oversig-ten knytter an til en tidligere oversigt fra 2002, som handler om sam-menhænge mellem læse- og regnevanskeligheder.Desuden har Lundberg og Sterner skrevet bogenRäknesvårigheteroch lässvårigheter: under de förste skolären – hur hänger de ihop?(2006), hvor deser på, hvordan læse- og regnevanskeligheder hænger sammen. Bogenbidrager med konkret råd om, hvordan elevernes vanskeligheder i for-bindelse med læsning og regning kan blive kortlagt, samt hvordan godvidensbaseret undervisning kan blive struktureret. Bogen indeholder be-skrivelser af øvelser og arbejdsmateriale, som kan anvendes i hverdagen.Med samme tema har de skrevet artiklen ”Hur hänger läs-svårigheter och matematiksvårigheter ihop” (2004), hvor formålet er atundersøge sammenhængen mellem matematik- og læsevanskeligheder,samt hvilke årsager der kan være disse. Udgangspunktet er, at der måfindes en fælles bagvedliggende faktor, som gør, at der både optræderlæse- og matematikvanskeligheder. Et bud på en fælles faktor er (lav)intelligens eller (dårlig) arbejdshukommelse, idet man både i forbindelsemed læsning og regning har brug for en velfungerende arbejdshukom-melse for at holde informationer i hovedet, mens man udfører andreoperationer. Forfatterne pointerer, at der ikke nødvendigvis er en sam-menhæng mellem læse- og matematikvanskeligheder, men at der er enrække aspekter, som vanskelighederne har til fælles.GÖREL STERNER (NCM, GÖTEBORG UNIVERSITET)

Brian Butterworth er professor i kognitiv neuropsykologi på Institute ofCognitive Neuroscience ved University College London. Hans forsk-ningstemaer er centreret omkring matematisk psykologi, ordblindhed ogtalevidenskab (speech science).Butterworths forskning strækker sig over emner som talefejl,korttidshukommelse, ordblindhed, matematik og dyskalkuli. I forhold tildyskalkuli er Butterworth optaget af børn og unges udvikling, med vægtpå udviklingen af forståelsen af numeriske koncepter (Butterworth, 2005).Butterworth er desuden grundlægger af og redaktør for tidsskrifterneMathematical CognitionogLanguage and Cognitive Processes.Aktuelt arbejder

Butterworth sammen med kollegaer på de neuropsykologiske og geneti-ske aspekter bag matematiske evner.Butterworth taler om den matematiske hjerne og læner sig op aden neurobiologisk årsagsforklaring og tilgang til talblindhed. Han erblandt de forskere, der mener, at talblindhed skyldes, at den neurobiolo-giske talsans mangler eller er forringet. På baggrund af hjerneforskningom forskellige hjerneskadetyper, hvor matematikvanskeligheder opstår(alkalkuli), mener han, at den matematiske evne sandsynligvis befindersig i parietallapperne.Butterworth har udviklet en screeningtest for at identificere mu-lige dyskalkulikere,Dyscalculia Screener(2003). Dertil har Butterworthsammen med Emersons House’s75matematiske direktør, Dorian Yeoudgivet bogenDyscaculia Guidance(2004). Bogen fungerer som en praktiskmanual til, hvordan man bedst støtter elever med specifikke regnevan-skeligheder. Der er tale om forskellige støtteformer for elever fra børne-haveklasse til universitetsniveau. Guiden består af både gode råd ogpraktiske aktiviteter, såsom leg og spil, der er kategoriseret efter specifik-ke matematiske områder.DIANA LAURILLARD

Steve Chinn er selvstændig konsulent, forsker og forfatter. Han er ud-dannet fysiker og har mange års erfaring med at undervise. Chinn harblandt andet ledet tre specialskoler for elever med ordblindhed og erderudover grundlægger af skolen Mark College, der er en drengeskole forordblinde, hvor han også var leder i 19 år. Han har desuden vundet flerepriser for sit arbejde med ordblindhed og matematikvanskeligheder. Haner også engageret i flere udvalg og foreninger særligt inden for dysleksi-området, men også dyskalkuli-området.Chin har flere udgivelser bag sig, særligt har han været engagereti dysleksi-området, men har også været meget aktive inden for områder-ne matematikvanskeligheder og dyskalkuli.Han har blandt andet undersøgt matematikangst blandt elever iEngland, hvor hans resultater viste, at mellem to til seks procent af alleelever lider af matematikangst. Derudover har han forsket i sammen-hængen mellem dysleksi og matematikvanskeligheder.Yderligere har han udviklet en test og diagnosticeringsmaterialefor matematikvanskeligheder og dyskalkuli og dertil en matematikangst-test for voksne.JAMES GILLUM

regnefærdigheder, samt hvilke dele af hjernen der bearbejder talinforma-tion og evnen til at regne.Ansari beskriver dyskalkuli som en specifik læringsvanskelighedinden for det matematiske domæne. Målet for hans forskning er at un-dersøge årsagen bag udviklingsmæssig dyskalkuli, herunder hvordan detudfolder sig og udvikler sig over tid, og på sigt hvordan børn med dennetilstand kan afhjælpes.Ansari fremhæver, at der findes en del information om, hvordanden voksne hjerne håndterer tal, men meget begrænset indsigt, i hvordanbørn løser matematiske opgaver, og hvilke hjernemekanismer der er in-volveret. Ansari begyndte derfor at undersøge, hvordan hjernen udfoldersig udviklingsmæssigt over tid, og hvordan vi på sigt kan støtte børn, derer påvirket af denne funktionsnedsættelse. Ved hjælp af hjernescanningersøger han indsigt i, hvilke hjernefunktioner der er aktive, når vi regner.Dertil undersøger han, hvordan hjernestruktur og hjernefunktion inter-agere, når vi efterhånden lærer og udvikler os. Som det er nu, bliver hjer-nefunktion og -struktur ofte undersøgt separat. Med nye visuelle tekno-logier er det muligt at kombinere vores viden om både struktur og funk-tion..DAVID C. GEARY

David Geary er ansat ved Institut for psykologi ved University of Mis-souri-Columbia. I 1990’erne begyndte Geary at interessere sig for for-holdet mellem kognitive funktioner og matematiske færdigheder. Hananvendte et omfattende testbatteri for at måle forskellige matematiskeydelser og forståelser. Hermed blev udtrykkene ”procedural kundskab”og ”begrebsmæssig kundskab” centrale i debatten, og det blev fremhævet,at begge former for kundskab var afgørende for matematisk færdighed(Lunde, 2012).Geary fremhæver blandt andet, hvordan kognitive og neuro-psykologiske træk præger forskellige former for matematikvanskeligheder.Han peger på svag hukommelse og kognitive funktioner som årsag tilmatematikvanskeligheder. Geary har påpeget, at det var sandsynligt, atbørn, på baggrund af at være begyndt i skole uden at have lært basalekundskaber om tal og uden at kunne tælle eller anvende strategier i for-hold til tal, fik dårligt udbytte af undervisningen

Ladsilav Kocs er en tjekkisk psykolog. I 1974 udførte Kocs det førstesystematiske studie med børn med matematikvanskeligheder. Resultater-ne viste, at dyskalkuli er en strukturel forstyrrelse af individets matemati-ske færdigheder.Kocs er ophavsmand til udtrykket ”udviklingsmæssig dyskalkuli”(developmental dyscalculia). I Tjekkoslovakiet baserede man specialpæ-dagogikken på sovjetisk defektologi, hvilket betød, at Kocs ikke kunnekalde det ”vanskeligheder i matematik”. Kocs blev derfor nødt til atknytte vanskelighederne til noget, der havde udviklet sig som et mentalthandicap, hvilket blev til det mere neutrale ”developmental dyscalculia”(Lunde, 2012). Med begrebet udviklingsmæssig dyskalkuli gør Kocs dy-skalkuli til et arveligt fænomen. Han definerer det som en forstyrrelse iden matematiske præstationsevne, hvilket skyldes en funktionsnedsættel-se i de områder af hjernen, som vedrører matematisk bearbejdning. Derer dog ingen funktionsnedsættelse i individets generelle mentale funktion.Han lægger vægt på, at det er den signifikante forskel mellem matematiskfærdighed og generel intelligens, der er afgørende. I 1970 defineredeKocs udviklingsmæssig dyskalkuli således:78. Tidligere publikationer kan ses her: http://udel.edu/~njordan/.79. http://www.huji.ac.il/dataj/controller/ihoker/MOP-TAFF_LINK?sno=5000 440&Save_t=.

A structural disorder of mathematical abilities that has its originin a genetic or congenital disorder of those parts of the brainthat are direct ... Psychological substrate of the maturation ofmathematical abilities adequate to age, without a simultaneousdisorder of general mental functions (Kocs, I: Lunde, 2012:13)I forhold til Kocs’ observationer af personer, der havde matematikvan-skeligheder på grund af deres situation, kaldte han det ”pseudo-dyskalkuli”.Han fremhævede også, at matematikvanskeligheder kunne redu-ceres via undervisning eller specialpædagogisk hjælp, og at den måde,eleverne gjorde brug af hjælpen på, var et led i diagnosticeringen.RUTH SHALEV

Mahesh Sharma er professor ved Cambridge College i Boston. Sharmatager udgangspunkt i begrebet dyskalkuli. Han anvender en bred definiti-on af begrebet, hvor han anser det for at være vanskeligheder med atmodtage, forstå og behandle kvantitative og spatiale informationer (Lin-denskov & Weng, 2004).I forhold til indikatorer på vanskeligheder omtaler han fx van-skeligheder med at betale og få penge tilbage, vanskeligheder med at fin-de ud af klokken eller aflæse et bykort (Lindenskov & Weng, 2004).Med hensyn til at støtte elever med dyskalkuli beskriver han trevigtige træk:

Alan Bishop har siden 1992 været lektor på Melbourne Universitet.In-den da var han lektorved Universitetet i Cambridgei 23 år.Han varformand forden britiske Mathematical Associationfra 1991-1992 og enaf grundlæggerne afBritish Educational Research Association. Bishopsforskning er centreret omkring matematikdidaktik, undervisning af elevermed anden etnisk baggrund, undervisning af tosprogede samt undervis-ning af handikappede. Bishop har lavet flere antropologiske studier i for-skellige kulturer, hvor han konkluderer, at der i alle kulturer eksistererseks grundlæggende aktiviteter, som matematiske begreber og operatio-ner vokser ud af og udvikles sammen med. De seks aktiviteter er at tælle,at måle, at lokalisere, at designe, at spille/lege og at forklare.

Danmark, Sverige, Norge, Finland og Island har oprettet det nordiskeforskernetværk NORSMA, hvor blandt andet matematikvanskelighederdiskuteres og forskningsresultater inden for emnet fremlægges. Netvær-ket har som formål at skabe større kendskab til området og større sam-menhæng mellem teori og praksis.Den første NORSMA-konference blev afholdt i 2012, hvor flereressourcepersoner fra de nordiske lande blev samlet til en konference.Dette blev startskuddet til NORSMA. Siden har netværkets medlemslan-de på skift holdt konferencen hvert andet år. I november 2013 afholdesden syvende NORSMA-konference i København. Arrangementet forlø-ber over tre dage – en læredag og to konferencedage.

En gruppe special- og matematiklærere har dannet foreningen DanSMa,for at styrke matematikken i specialundervisningen. Matematikforenin-gen DanSMa (Dansk Special Matematik) er for alle, der interesserer sigfor og underviser i matematik, og netværket dækker alle klassetrin. Lek-tor ved læreruddannelsen i Holbæk, Bent Lindhardt, er formand for for-eningen, som består af læse-tale-hørepædagoger, specialpædagogiskekonsulenter, folkeskolelærere, læreruddannere og voksenundervisere.Foreningens formål er at varetage professionsfaglige interesser i relationtil undervisning af børn og voksne med særlige behov i matematik. Detskal blandt andet ske ved at igangsætte offentlige debatter om relateredeproblemstillinger og udbrede kendskabet til de nyeste forskningsresulta-ter om, hvad matematikvanskeligheder er, og hvordan man diagnostice-rer og underviser børn, unge og voksne med matematikvanskeligheder(folkeskole.dk, 2011).

BEGREBER

Akalkuli:

Betyder ”helt talblind” (til sammenligning betyder dyskalku-li ”mangelfuld regneevne”). Der er tale om en manglende evne til at ar-bejde med tal grundet en erhvervet hjerneskade. Trods massiv øvelse kanman ikke tillære sig de grundlæggende principper for regning. Gruppenaf personer med akalkuli udgør kun en promille af befolkningen (Lunde,2006; Adler 2003, 2008).

Aritmetik:

En gren af matematikken, der dækker over de basale regne-færdigheder og de grundlæggende regneregler eller traditionelle operatio-ner addition, subtraktion, multiplikation og division. Kan også indeholdede lidt mere avancerede færdigheder inden for matematikken, men knyt-tes oftest til de fire ovennævnte operationer. Aritmetik er inddraget idenne oversigt, da det er dette område, der ifølge flere videnspersoner(blandt andet Butterworth) skaber mange problemer for dyskalkulikere.Således kan flere være gennemsnitlige eller over gennemsnittet til andregrene af matematikken, fx geometri. Men den grundlæggende talforståel-se og simpel aritmetik driller folk med dyskalkuli.

Developmental dyscalculia

(Udviklingsmæssig dyskalkuli): ”udvik-lingsmæssige dyskalkuli refererer til en matematikvanskelighed en personer født med. Dette er for at adskille det fra erhvervet dyskalkuli, hvilket

er forårsaget af hjerneskade” (egen oversættelse, Emerson & Babtie2010).80

Dyskalkuli:

(Vores definition) Dyskalkuli er en funktionsnedsættelse,der kan have negativ indvirkning på den berørtes uddannelses- og ar-bejdsliv. Tilstanden drejer sig om tilbagestående regnefærdigheder, somikke modsvares af tilsvarende tilbagestående færdigheder på andre felter.De specifikke regnevanskeligheder omfatter påfaldende vanskelighedermed at forstå og håndtere basal talbehandling, såsom at sammenligne talog mængder eller tælle små antal genstande. I forlængelse heraf er dertale om påfaldende vanskeligheder ved addition, subtraktion, multiplika-tion og division. Tilstanden kan fx komme til udtryk ved vanskelighedermed at aflæse et analogt ur, finde et husnummer eller forstå en togplan.Tilstanden omfatter ikke nødvendigvis vanskeligheder med mere abstrak-te matematiske færdigheder i algebra, trigonometri, geometri og kom-plekse beregninger. Dyskalkulikere vil ofte udvise gode eller middel præ-stationer ved abstrakte matematiske færdigheder. Dyskalkuli er som ud-gangspunkt ikke en konsekvens af øvrige vanskeligheder, det forholdersig snarere omvendt. Dyskalkuli kan fører til sekundære vanskeligheder,såsom angst og dårligt selvværd. Dyskalkuli skyldes ikke mental retarde-ring eller mangelfuld skolegang. Dog kan tilstanden omfatte kognitiveproblemer, som mangelfuld semantisk- og arbejdshukommelse (jf. kapi-tel 3).

Livsmatematik:

Her danner elevernes erfaringer i dagligdagen grundlagfor læringen. Eleverne kan i højere grad relatere til matematikken, nården er baseret på møder med, bearbejdelse af og beslutninger i hverda-gen. Elevens hverdagserfaringer med husholdning, tøj, naturen, indkøb,samfundet, fritidsinteresser mv. skal med andre ord anvendes. Begrebeter udviklet af Oluf Magne (Magne 2003).

Matematikmestring:

Et begreb af Olav Lunde, som modsat begre-bet ”matematikvanskeligheder” skal afværge den ensidige fokusering pådet, der ikke vil lykkes. Lunde anvender betegnelsen ”behov for tilrette-lagt læring af matematikmestring for elever med særlige behov i matema-tik”. Betegnelsen understreger, at vanskeligheden ikke er noget givet ved80. “Developmental Dyscalculia refers to a maths difficulty that a child is born with. This is to dis-tinguish it from acquired dyscalculia, which is caused by accidental brain damage”.

eleven, men at eleven i samspil med læreren, forældre, omgivelser skallære at mestre matematikken.

Matematikvanskeligheder:

Repræsenterer et brud på den jævne ogkontinuerlige faglige udvikling, som de fleste elever følger. Med andreord er eleven stagneret eller gået tilbage i matematik i forhold til en nor-mal faglig udvikling. Matematikvanskeligheder er en bredere betegnelseend dyskalkuli, som omhandler problemer inden for specifikke områderaf matematikken. Karakteristiske træk for matematikvanskeligheder erbesvær med kvantitativ læring, dvs. at eleven kan have problemer medrumforståelse, visuel perception, symbolgenkendelse, hukommelse, tæl-ling samt kognitive strategier. Der kan være flere former for matematik-vanskelighede: forstyrrelser i systematisk tænkning og rumforståelse, dår-lige indlæringsmåder, svag begrebsforståelse samt svag evne til automati-sering (Lunde 2006; Ostad, 1990).

Pseudo-dyskalkuli:

Et udtryk især brugt af Adler, som dækker overpsykologiske årsagsfaktorer. Vanskelighederne har her grobund i følel-sesmæssige blokeringer hos barnet. Barnet besidder kognitive, tanke-mæssige ressourcer til at kunne lykkes med matematik, men har tilegnetsig den opfattelse, at hun/han ikke kan blive dygtig til emnet. Alle bar-nets eventuelle mislykkede forsøg bekræfter denne opfattelse. I gruppenses en overvægt af piger (Adler, 2003).

Regnehuller:

Betegner de afgrænsede områder, som barnet opleverproblemer med, samtidig med at begrebet indikerer, at der er noget rundtom hullerne, som ikke er problematisk. Begrebet skal støtte en opfattelseaf, at matematikvanskeligheder ikke er totale, men at det faglige indhold ivanskelighederne kan afgrænses og præciseres. Begrebet skal ligeledesinvitere til at lokalisere hullerne og til at fylde dem ud, bygge bro overeller finde/skabe vej udenom (Lindenskov & Weng)

Basal talforståelse (inkl.Gruppe/klasse.positionssystemet).LINU matematikscreeningAutomatisering af de firePC-baseret.regnearter.Opmærksomhed og ar-bejdshukommelse.Evnen til sekventiel og spa-tial organisering.Tidsforbrug.Olav Lunde:Talforståelse, addition,Individuel/klasse.subtraktion, problemløs-Rummelig matematikning, hukommelse, kon- Foretages af fx matematik-centration, opmærksom-vejleder, lærer.hed, før-faglige begreber,rum-retning, form og stør-relse.Michael Wahl Andersen:Talforståelse, addition,Individuel/klasse.subtraktion, problemløs-Matematik for migning, hukommelse, kon- Foretages af fx matematik-centration, opmærksom-vejleder, lærer.hed, før-faglige begreber,rum-retning, form og stør-relse.Hilde Skaar, Inger Kristine Leg, hvor matematiskeObservation af matematiskaspekter indgår.Løge, Olav Lunde, Elinaktivitet via leg og hver-Reikerås og Tone Dalvang:dagsaktiviteter.

Formålet er at identificere og vur- Øvelserne til opfølg-dere børn med behov for støttening skal styrkesamt opfølgende undervisning.elevens grundlæg-Består af:gende forståelseSkriftligt materiale med forskellige for tal, addition,subtraktion og ma-forslag til øvelser, som er struk-tematikkens an-tureret efter det niveau, elevenvendelse. For ni-viser sig at være på ved den ind-ledende test, henholdsvis niveau veau 1 gælder tal-området 1-20. For1, 2 og 3.niveau 2, talområ-Øvelserne er struktureret i syvdet 1-50. Niveau 3faglige områder med progressi-for talområdet 0-on.100.

Hvornår skal der testes? Formål og eventuel opfølgningBemærkningerCa. 7-10 årFormålet med de tre screeninger Matematikscreeningener at vurdere børns kognitive ud- må ikke anvendes iso-(indskoling – mellemtrin).vikling. Opfølgende har Adlerleret. Adler anbefaler,udviklet en idébog:Kognitiv træ-at den anvendesning matematik.sammen medEvnenCa. 11-15 årtil hurtigt at AfgøreFokus er på de samme ti delom-(mellemtrin – udskoling).råder, som der testes i. De inde-Mængder,Færdig-hedstestogTalserier.holder alle emner (kognitiveprocesser), der har betydning forarbejdet med matematik. HverCa. 16 år og opefter.delområde indeholder opgaveraf forskellige sværhedsgraderog indeholder både færdige op-gaver og opgaver, hvor elevenselv skal konstruere opgaven.Materialet er tænkt som et idé-oplæg, hvorfra læreren (gerne isamarbejde med eleven) kankonstruere egne opgaver.

Udføres typisk af lærere.Evnen til hurtigt at afgøre Gruppetest eller som led i 6 år og opefter (til voksne).størrelsen af mindreen individuel vurdering afEvnen til Hurtigt at Afgøremængder.elever.MængderLena Lindeskov & PeterTalforståelse, de fire reg- Individuel/små grupper.Uafhængig af klassetrinWengningsarter, del-helhed(materialet er knyttet tiludvikling af de matemati-Matematikvanskeligheder –begrebet, geometriskeAlle kan teste. Matematik-former og figurer, måling. lærere kan anvende ma-ske begreber, men fokustidlig interventioner på det matematiskeFokus på strategi -terialet. Anvendelsen viltænkning og problembe-kunne optimeres gennem indhold på 1-7. klasse-trin).handling.deltagelse i lærerkursetom materialet, og hvor-dan det tilpasses konkre-te elever.

Formålet er at vurdere børns for- Lindenskov og Wengudsætninger, potentialer, behovanvender beteg-og motivation med henblik på en nelsen ”regnehul-tidlig intervention, når en elevler”, som omfatter,indikerer at være i vanskelighe-neurologiske, psy-der samt en generel tidlig ind-kologiske, sociolo-sats på begyndertrinnet.giske og didaktiskeForslag til undervisningsaktiviteter perspektiver.til konsoliderende læring i ele-vens sikre områder og til viderelæring.(Uidentificeret om det er(Uidentificeret målgruppe). Formålet er at teste elever, i hvilkeindividuel eller klassestrategier de bruger og er med tiltest).at kortlægge, om elever er ved atudvikle matematikvanskelighe-Lærere, PPT og Specialpæ-der.dagoger.

148Hvornår skal der testes?Ca. 7-11 år(1.-4. klasse).Ca. 8-13 år(3. og 6. klasse).Ca. 6-10 år(1.-3. klasse).Ca. 9-12 år(4.-5. klasse).Formålet er at vurdere klassens ogden enkelte elevs standpunktefter pågældende trin.Formål og eventuel opfølgningFormålet er at støtte eleverneslæreprocesser undervisning.Alle kan teste – udførestypisk af lærere.Alle kan teste – udførestypisk af lærere.Individuel/klasse.Alle kan teste – udførestypisk af lærere.Formålet er at vurdere elevensfaglige formåen og matematiskeudvikling.Formålet er at vurdere elevernesniveau og placering af elevernepå niveau.

LITTERATURAarhus Universitet (2011):TIMSS undersøgelsen 2011. En sammenfatning.Trends in International Mathematics and Science Study.Aarhus: AarhusUniversitet.Adams, J.W. & G.J. Hitch (1997): “Working memory and children'smental addition”.Journal of Experimental Child Psychology,67(1), s.21-38.Adler, B. (2008):Dyskalkuli & matematik. En håndbog i matematikvanske-ligheder.Specialpædagogisk Forlag.Adler, B. (2005):Vad är dyskalkyli? En bok om matematiksvårigheter.Höllvi-ken: NU-förlaget.Adler, B. (2003):”Dyskalkyli – Matematiksvårigheter”.Lärartidning.Adler, B. (2000):Matematikscreening. Info om en undersökningsmetod.Tilgæn-gelig på: http://www.dyskalkyli.nu/matematikscreening.html.Besøgt 1-9-0013.Adler, B. & Holmgren, H. (2003):Neuropædagogik - om kompliceret læring.Vejle: Krogh.Alarcón, M., J.C. DeFries, J.G. Light & B.F. Pennington (1997): “A TwinStudy of Mathematical Disability”.Journal of Learning Disabilities,30(6), s. 617-623.Alrø, H., M. Blomhøj, H. Bødtkjer, I.M. Christensen, K. Jess, O. Skovs-mose, M. Skånstrøm, P. Valero, T. Wedege, L.Ø. Johansen, L.

Lindenskov & B.D. Søndergaard (2006):Kunne det tænkes? - ommatematiklæring.København: Akademisk Forlag.American Psychiatric Association (2013):DSM-5 Development28-6-0013.Andersen, M.W. (2004):“Democracy and Participation. A Challenge for SpecialNeeds Education in Mathematics”.Paper præsenteret på konfer-encen Proceedings of the 2ndNordic Research Conference onSpecial Needs Education in MathematicsAndersen, M.W. (2009):“Different Learners – Different Math?”.Paperpræsenteret på konferencen Proceedings of the 4th Nordic Re-search Conference on Special Needs Education in MathematicsAndersson, A. (1984):Barn med matematikproblem.Kalmar: Institut för lä-rarutbildningAssessment & Development Matters (2012): 4(3).Ayres, A. J. (2007):Sanseintegration hos børn.Hans Reitzels Forlag.Berteletti, L., D. Lucangeli, M. Piazza, S. Deheane & M. Zorzi (2010):“Numerical Estimation in Preschoolers”.Developmental Psychology,46(2), s. 545-551.Bird, R. (2009):Overcoming Difficulties with Number. Supporting Dyscalculia andStudents who Struggle with Maths.London: SAGE Publications Ltd.Bird, R. (2007):The Dyscalculia Toolkit. Supporting Learning Difficulties inMaths.London: Paul Chapman Publishing.Björnström, M. (2012):Värt att veta om dyskalkyli.Stockholm: Natur &kultur.Björnström, M. (2010):UR Samtiden - Underbar matematik. Vad vet vi omdyskalkyli?Sveriges Utbildningsradio.Breznitz, Z., O. Rubinsten, V.J. Molfese & D.L. Molfese (2012):Reading,Writing, Mathematics and the Developing Brain: Listening to Many Voic-es.Dordrecht: Springer.Butterworth, B. (2013): “Developmental Dyscalculia”. I: Campbell, J.I.D.:Handbook of Mathematical Cognition.New York: Psychology Press,s. 455-467.Butterworth, B. (2012):UR Samtiden - När siffrorna bråkar. Dyskalkyli - såfunkar det.Sveriges Utbildningsradio.Butterworth, B. (2012):UR Samtiden - När siffrorna bråkar. Dyskalkyli - attförstå och hjälpa eleverna.Sveriges Utbildningsradio.Butterworth, B. (2010): “Foundational Numerical Capacities and the Or-igins of Dyscalculia”.Trends in Cognitive Sciences,14(12), s. 534-541.

Butterworth, B. (2005): “The development of arithmetical abilities”.Jour-nal of Child Psychology & Psychiatry,46(1), s. 3-18.Butterworth, B. (2003):Dyscalculia Screener. London.nferNelson PublishingCompany Limited.Butterworth, B. (1999):The Mathematical Brain.London: Macmillan Pub-lishers Ltd.Butterworth, B., S. Varma & D. Laurillard (2011): “Dyscalculia: FromBrain to Education”.Science,332, s. 1049-1053.Butterworth, B. & D. Yeo (2004):Dyscalculia Guidance. Helping Pupils withSpecific Learning Difficulties in Maths.London: David Fulton.Böttger, H., G. Kvist-Andersen, L. Lindenskov & P. Weng (2003):“De-mocracy and Participation. A Challenge for Special Needs Education inMathematics”.Paper præsenteret på konferencen Proceedings ofthe 2nd Nordic Research Conference on Special Needs Educa-tion in MathematicsCallaway, E. (2013): “Number Games”.Nature,493, s. 150-153.Caramazza, A. (1990):Cognitive Neuropsychology and Neurolinguistics: Advancesin Models of Cognitive Function and Impairment.Hillsdale, N.J.: Law-rence Erlbaum Associates.Causier, H. (2008): “Review of 'The Dyscalculia Toolkit: SupportingLearning Difficulties in Maths’”.Support for Learning, 23(4),s.214-214.Center for Undervisningsmidler (2009):En oversigt over evaluerings- og test-materialer til matematik.Odense: University College LillebæltChinn, S. (2012):More Trouble with Maths. A complete guide to identifying anddiagnosing mathematical difficulties.Routledge.Chinn, S. (2011):The Fear of Maths. How to Overcome It. Sum Hope 3.UnitedKingdom: Souvenir Press Ltd.Chinn, S. (2011):The Trouble with Maths. A Practical Guide to Helping Learn-ers with Numeracy Difficulties.London: Routledge.Chinn, S. (2009): “Mathematics Anxiety in Secondary Students in Eng-land”.Dyslexia,15(1), s. 61-68.Chinn, S. (2007):Dealing with Dyscalculia. Sum Hope�.London: SouvenirPress.Chinn, S. (2005):Maths and Dyslexia. A View from the UK. Tilgængelig påhttp://www.learning-works.org.uk/chinns-uk-research-pdf.Besøgt 4-7-2013.

Chinn, S. & J.R. Ashcroft (2006):Mathematics for Dyslexics. Including Dyscal-culia.Chichester: John Wiley & Sons, Ltd.Chinn, S. & J.R. Ashcroft (1993):Mathematics for Dyslexics. A TeachingHandbook.London: Singular Speech Pr.Coch, D., G. Dawson, K.W. Fischer (2010):Human Behavior, Learning, andthe Developing Brain.Atypical Development.New York: The GuilfordPress.Cohen Kadosh, R. & V. Walsh (2007): “Dyscalculia”.Current Biology,17(22), s. 946-947.Cohn, R. (1968): “Developmental Dyscalculia”.Pediatric Clinics of NorthAmerica, 15(3),s. 651-668.CSV Sydøstfyn(2009):Talblindhed/dyskalkuli.Tilgængelig på:http://www.dyskalkuli.dk. Besøgt 1-7-2013.Evans, R. & K. Goodmann (1995): “A Review of Factors Associatedwith Young Children's Difficulties in Acquiring Age-Appropriate Mathematical Abilities”.Early Child Development andCare,114, s. 81-95.Dalvang, T. (2004):“Democracy and Participation. A Challenge for SpecialNeeds Education in Mathematics”.Paper præsenteret på konfer-encen Proceedings of the 2ndNordic Research Conference onSpecial Needs Education in MathematicsDalvang, T. & E. Daland (2009):“Different Learners - different Math?”.Pa-per præsenteret på konferencen Proceedings of the 4th NordicResearch Conference on Special Needs Education in Mathemat-icsD'Angiulli, A. & L.S. Siegel (2003): “Cognitive Functioning as Measuredby the WISC-R: Do Children with Learning Disabilities HaveDistinctive Patterns of Performance?”Journal of Learning and Dis-abilities,36(1), s. 48-58.Davis, R.D. & E.M. Braun (2003):The Gift of Learning. Proven New Methodsfor Correcting ADD, Math & Handwriting Problems.New York: Per-igee Trade.Devine, A, F. Soltész, A. Nobes, U. Goswami & D. Szucs (2013): “Gen-der Differences in Developmental Dyscalculia Depend on Diag-nostic Criteria”.Learning and Instruction,27, s. 31-39.Dowker, A. & L. Kaufmann (2009): “Atypical Development of Numeri-cal Cognition: Characteristics of Developmental Dyscalculia”.Cognitive Development,24(4), s. 339-342.

Dowker, A. (2001): “Numeracy Recovery: A Pilot Scheme for Early In-tervention with Young Children with Numeracy Difficulties”.Support for Learning,16(1), s. 6-10.Dumontheil, I. & T. Klingberg (2012): “Brain Activity during aVisuospatial Working Memory Task Predicts Arithmetical Per-formance 2 Years Later”.Cerebral Cortex,22, s. 1078-1085.Engström, A. & O. Magne (2004):“Democracy and Participation. A Challengefor Special Needs Education in Mathematics”.Paper præsenteret påkonferencenProceedings of the 2ndNordic Research Conference on Spe-cial Needs Education in MathematicsEngström, A. (2003):Specialpedagogiska frågeställningar i matematik - En in-troduktion.Örebro: Pedagogiska institutionen, Örebro universitet,8.Emerson, J., & P. Babtie (2011):The Dyscalculia Assessment.London: Con-tinuum International Publishing Group.EMU Danmarks Undervisningsportal (2012):Matematikken svigtes i special-pædagogiskbistand.Tilgængeligpå:http://www.emu.dk/modul/matematikken-svigtes-i-specialp%C3%A6dagogisk-bistand. Besøgt 16-7-2013.European Agency for Development in Special Needs Education (Agency)(2013):Organisation of Provision to Support Inclusive Education - Litera-ture Review.Odense, Danmark: European Agency for Develop-ment in Special Needs Education.Farrell, M. (2006):The Effective Teacher's Guide to Dyslexia and Other SpecificLearning Difficulties. Practical Strategies.London: Routledge.Furness, A. (1992):Mätaren. Lärarhandledning.Solna: Ekelund.Geary, D.C. (2004): “Mathematics and Learning Disabilities”.Journal ofLearning Disabilities,37(1), s. 4-15.Geary, D.C. (1993): “Mathematical Disabilities: Cognition, Neuropsy-chological and Genetic Components”.Psychological Bulletin,114(2),s. 345-362.Gersten, R., B. Clarke & M.M. Mazzocco (2007): “Historical and Con-temporary Perspectives on Mathematical Learning Disabilities”.I: M.M. Mazzocco & D.B. Berch (red.):Why Is Math So hard ForSome Children? The Nature and Origins Of Mathematical Learning Dif-ficulties and Disabilities.Baltimore: Brookes Publishing, s. 7-28.Gillum, J. (2012): “Dyscalculia: Issues for Practice in Educational Psy-chology”.Educational Psychology in Practice,28(3), s. 287-297.

Gisterå, E.M. (1995):Dyslexi och dyskalkyli: Utvärdering av läromedelskassetterför elever med läs- och skrivsvårigheter.Uppsala: Pedagogiska institu-tionen.Gordon, N. (1992): “Children with Developmental Dyscalculia”.Devel-opmental Medicine & Child Neurology,34, s. 459-463.Gross, J. (2007): “Supporting Children with Gaps in Their MathematicalUnderstanding: The impact of the National Numeracy Strategy(NNS) on Children who find Mathematics Difficult”.Educationaland Child Psychology,24(2), s. 146-156.Grynberg, S. (2010):Ta1 b1inde e1ever b1iver overset.Tilgængelig på:http://www.folkeskolen.dk/62901/ta1b1inde-e1ever-b1iver-overset. Besøgt d. 3-9-2013.Hale, J.B., C.A. Fiorello, M. Bertin & R. Sherman (2003): “PredictingMath Achievement through Neuropsychological Interpretationof WISC-III Variance Components.".Journal of PsychoeducationalAssessment,21, s. 358-380.Hannell, G. (2013):Dyscalculia. Action plans for Successful Learning in Mathe-matics.London: Routledge.Hansen, H.C. & B. Petersen (2006):Der er mere end ét svar – matematik ogspecialundervisning.København: Alinea.Henderson, A. (2012):Dyslexia, Dyscalculia and Mathematics. A practical guide.London: Routledge.Henderson, A., M. Brough & F. Came (2003):Working with Dyscalculia.Recognising Dyscalculia Overcoming Barriers to Learning in Maths.Marlborough: Learning Works International.Herriot, S.T. (1967):The Slow Learner Project. The Secondary School 2 ”Slowlearner” in Mathematics.Stanford, Californien: Leland Stanford Ju-nior University.Horsens Kommune, Børn og Unge. (2011):Tidlig identificering af elever imatematikvanskeligheder - Inspirationsmateriale.Horsens: HorsensKommuneHoussart, J. (2004):Low Attainers in Primary Mathematics. The Whisperers andthe Maths Fairy.London & New York: RoutledgeFalmer.Håkansson, L. (1999):Inlärningsproblem och arbetsplatsanpassning - utvecklings-betingad dyslexi, dysgrafi, dyskalkyli, dysmnesi. En fallstudie.Solna: Ar-betsmarknadsservice, Arbetgsmarknadsstyrelsen (AMS).Jakobsson, I.L. & I. Nilsson (2011):Specialpedagogik och funktionshinder.Stockholm: Natur & kultur.

James, A.N. (2009):Teaching the Female Brain. How Girls Learn Math andScience.Thousand Oaks, Californien: Corwin.Jensen, A. (2002):”En matematikk for alle i en skole for alle”.Paper præsen-teret på konferencen Rapport fra det 1. nordiske forskerseminarom matematikkvansker. Kristiansand, 25-28. september 2001.Johansen, L.Ø. (2007):Matematiklæreren som sproglærer.Institut for Uddan-nelse, Læring og Filosofi, Aalborg Universitet: Aalborg Universi-tet. Ph.d.-afhandling.Johansen, L.Ø. (2006): ”Dyskalkuli - er det et overset problem?”Special-pædagogik,26(6), s. 2-9.Johansen, L.Ø. (2006): ”Matematikvanskeligheder – hvad er det?”. I:Skovsmose, O. & M. Blomhøj (red.):Kunne det tænkes? - om mate-matiklæring.Danmark: Malling Beck, s. 139-158.Johansen, L.Ø. (2002):”En matematikk for alle i en skole for alle”.Paperpræsenteret på konferencen Rapport fra det 1. nordiske forsker-seminar om matematikkvansker. Kristiansand, 25-28. september2001.Johnsen, F. (2004): ”Matematikkangst og ”blokkeringer””.Spesialpedago-gikk,2.Jordan, N.C., J. Glutting, N. Dyson, B. Hassinger-Das & C. Irwin (2012):"Building Kindergartners' Number Sense: A Randomized Cont-rolled Study”.Journal of Educational Psychology,104(3), s. 647-660.Kaufmann, L. & M.V. Aster (2012): “The Diagnosis and Management ofDyscalculia”.Deutsches Ärzteblatt International,109(45), s. 767-778.Kay, J. & D. Yeo (2003):Dyslexia and Maths.London: David FultonPublishers.Klingberg, T. (2012):UR Samtiden - Så minns unga. Gener, hjärnan och barnsutveckling.Sveriges Utbildningsradio.Klingberg, T. (2011):En bok, en författare. Torkel Klingberg.Sveriges Ut-bildningsradio.Kocs, L. (1974): “Developmental Dyscalculia”.Journal of Learning Disabili-ties,7 (3), s. 164-177.Kousholt, K. (2009):Evalueret. Deltagelse i folkeskolens evalueringspraksis.Danmarks pædagogiske universitetsskole, Århus Universitet,København.Krogshøj, L., M. Iversen & H. Brandt (2009):Matematik i sammenhæng meddysleksi.Ballerup: Ordblindeinstituttet.

Kunnskapsdepartementet (2000):Studenter med spesifikke lese-, skrive- ellermatematikkvansker. Utredning om problemstillinger knyttet til studiesitu-asjonen.Tilgængelig på:http://www.regjeringen.no/nb/dep/kd/dok/rapporter_planer/rapporter/2000/studenter-med-spesifikke-lese-skrive-ell.html?id=105558. Besøgt d. 10-8-2013.Landerl, K., A. Bevan & B. Butterworth (2004): “Developmental Dyscal-culia and Basic Numerical Capacities: A Study of 8--9-Year-OldStudents”.Cognition,93(2), s. 99-125.Larsen, M.S., C.B. Dyssegaard & N. Tiftkci (2013):Effekt og pædagogiskindsats ved inklusion af børn med særlige behov i grundskolen - systematiskreview.København: Dansk Clearinghouse for Uddannelsesforsk-ning, Aarhus Universitet.Lever, M. (2003):Shape and Space. Activities for Children with MathematicalLearning Difficulties.London: David Fulton Publishers.Lindekvist, A.L. (2004):Specifika matematiksvårigheter - Dyskalkyli. En litte-raturöversikt.Institutionen för matematik och naturvetenskap,Högskolan Kristiansand. Ph.d.-afhandling.Lindenskov, L. (2010): ”Introduktion til matematikvanskeligheder - bag-grund og begreber”.Matematik,1.Lindenskov, L. (2007):“Mathematics Teaching and Inclusion”.Paperpræsenteret på konferencen. Proceedings of the 3rd Nordic Re-search Conference on Special Needs Education in Mathematics.Lindenskov, L. (2007): ”Samarbejde mellem matematiklærere og psyko-loger om matematikvanskeligheder”.Psykologisk Pædagogisk Råd-givning,44(4), s. 305-323.Lindenskov, L., P. Weng & N. Egelund (2006): ”Matematik - uddybendeanalyser”. I: N. Egelund & T.Y. Andersen (red.):PISA og de 161/2-årige uddannelsessøgende. Overordnede resultater, uddybende analyserog metode.København: Danmarks Pædagogiske Universitets For-lag, s. 21-26.Lindenskov, L. & P. Weng (2013):Matematikvanskeligheder. Tidlig interventi-on.København: Dansk Psykologisk Forlag.Lindenskov, L. & P. Weng (2009):“Different Learners – different Math?”.Paper præsenteret på konferencen Proceedings of the 4th Nor-dic Research Conference on Special Needs Education in Math-ematics.

Lindenskov, L. & P. Weng, P. (2009): ”Specialundervisning i matematik:Kan det ikke være lige meget?”. I: T. Susan & S. Langager (red.):Specialpædagogik i skolen. En grundbog.København: Gyldendal, s.211-230.Lindenskov, L. & P. Weng, P. (2007):“Mathematics Teaching and Inclusion”.Paper præsenteret på konferencen Proceedings of the 3rd Nor-dic Research Conference on Special Needs Education in Math-ematics.Lindenskov, L. & P. Weng (2006): ”Matematikvanskeligheder og regne-huller?”.MONA. Matematik- og Naturfagsdidaktik - tidsskrift for un-dervisere, forskere og formidlere2, s. 90-93.Lindenskov, L. & P. Weng (2006): ”Regnehuller og addition: Hvad børman som lærer være opmærksom på i indskolingsmatematikkenfor at undgå at en elev møder et ’regnehul’ ?”.Spesialpedagogikk,71(4), s. 12-17.Lindenskov, L. & P. Weng (2005): ”Matematikvanskeligheder og lavtpræsterende elever i Danmark”.MONA.Matematik- og Naturfags-didaktik - tidsskrift for undervisere, forskere og formidlere,2, s. 56-75.Ljungblad, A.L. (2003):Att möta barns olikheter. Åtgärdsprogram och matema-tik.Varberg: Argument Förlag.Ljungblad, A.L. (2001):Att räkna med barn med specifika matematiksvårigheter.Varberg: Argument Förlag.Lundberg, I. & G. Sterner (2009):Dyskalkyli - finns det? Aktuell forskningom svårigheter att förstå och använda tal.Göteborg: Nationellt cen-trum för matematikutbildning, Göteborgs Universitet.Lundberg, I. & G. Sterner, G. (2008):Regne- og læsevanskeligheder i de førsteskoleår - hvordan hænger de sammen?Gylling: Alinea.Lundberg, I. & Sterner, G. (2006): "Reading, Arithmetic, and Task Ori-entation - How are they Related?".Annals of Dyslexia, 56(2),s.361-377.Lundberg, I. & G. Sterner (2002):Läs- och skrivsvårigheter och lärande i ma-tematik.Göteborg: Nationellt Centrum för Matematikutbildning,Göteborgs Universitet.Lunde, O. (2012):Når tal gi´r kaos. Specialpædagogisk fokus på matematikvan-skeligheder.Special-pædagogisk forlag i samarbejde med danskespecialmatematik.Lunde, O. (2008a): ”Kan vi forebygge matematikkvansker? Ja, det kanvi!”.Nämnaren,1, s. 16-20.

Lunde, O. (2008b): ”Matematikkvansker - samspillet mellom språk ogmatematikkvansker”.”Sprog og matematik - matematikkens sprog”Temahæfte.,s. 5-12.Lunde, O. (2006): ”Lærevansker i matematikk - En spesialpedagogiskutfordring for PPR!”.Psykologisk Pædagogisk Rådgivning,43(1), s.14-28.Lunde, O. (2004):“Democracy and Participation. A Challenge for Special NeedsEducation in Mathematics”.Paper præsenteret på konferencen Pro-ceedings of the 2ndNordic Research Conference on SpecialNeeds Education in Mathematics.Lunde, O. (2002):”En matematikk for alle i en skole for alle”.Paper præsen-teret på konferencen Rapport fra det 1. nordiske forskerseminarom matematikkvansker. Kristiansand, 25-28. september 2001.Lunde, O., K. Hole & A. Hansen, (1999):Lærevansker i norsk og matema-tikk: refleksjoner om likheter og ulikheter som grunnlag for spesialpedagogi-ske tiltak.Norge: PP-tjenestens materiellservice.Lunde, O. (1997):Kartlegging og undervisning ved lærevansker i matematikk:Bob-Kåres vei gjennom matematikkens verden.Klepp: Info vest Forlag.Lunde, O. (1994):Lærevansker i matematikk. En litteraturstudie om hvorfornoen barn er svake regnere og hva det medfører for skolens spesialundervis-ning.Klepp: Info Vest Forlag.Magne, O. (1998):Att lyckas med matematik i grundskolan.Lund: Studentlit-teratur AB.Magne, O. (2006): “Historical aspects on special needs education inmathematics.”Nordic Studies in Mathematics Education.Vol. 11(4)7-35.Magne, O. (2004):“Democracy and Participation. A Challenge for Special NeedsEducation in Mathematics”.Paper præsenteret på konferencen Pro-ceedings of the 2ndNordic Research Conference on SpecialNeeds Education in Mathematics.Magne, O. (2003):Literature on Special Educational Needs in Mathematics.Malmö: School of Education, Malmö.Magne, O. (2002):”En matematikk for alle i en skole for alle”. Paper præsenteretpå konferencenRapport fra det 1. nordiske forskerseminar om ma-tematikkvansker. Kristiansand, 25-28. september 2001.Magne, O. (1998):Att lyckas med matematik i grundskolan.Lund: Studentlit-teratur AB.

Magne, O. (1994):Dysmatematik. Den framtida skolans matematik för elevermed särskilda utbildningsbehov.Malmö: Lärarhögskolan.Magne, O. (1967):Matematiksvårigheter hos barn i åldern 7-13 år.Stockholm:Svensk Läraretidnings Förlag.Malmer, G. (2003):Analyse af læseforståelse i problemløsning - screeningtest ALPnr 1-8, fra 2. skoleår og op til voksne elever.Esbjerg: Svensk-NorskBogimport.Malmer, G. (2002):”En matematikk for alle i en skole for alle”.Paper præsen-teret på konferencen Rapport fra det 1. nordiske forskerseminarom matematikkvansker. Kristiansand, 25.-28. september 2001.Malmer, G. (2000): “Mathematics and Dyslexia – An Overlooked Con-nection”.Dyslexia, 6(4),s. 223-230.Malmer, G. (1999):Bra matematik för alla. Nödvändig för elever med inlärnings-svårigheter.Lund: Studentlitteratur.Malmer, G. & B. Adler (1996):Matematiksvårigheter och dyslexi. Erfarenheteroch synpunkter i pedagogisk och psykologisk belysning.Lund: Studentlit-teratur.Mastropieri, M.A. & T.E. Scruggs (2005):Cognition and Learning in DiverseSettings.Bingley: Emerald Group Publishing Limited.Mazzocco, M.M. & D.B. Berch (2007):Why Is Math So Hard For SomeChildren? The Nature and Origins of Mathematical Learning Difficultiesand Disabilities.Pennesylvania: Paul H. Brookes Publishing Co.Mazzocco, M.M. & R.E. Thompson (2005): “Kindergarten Predictors ofMath Learning Disability”.Learning Disabilities Research & Practice,20(3), s. 142-155.Miles, T.R. & E. Miles (2004):Dyslexia and Mathematics.London:RoutledgeFalmer.Munn, P. & R. Reason (2007): “Arithmetical Difficulties: Developmentaland Instructional Perspectives”.Educational and Child Psychology,24(2), s. 5-15.Munro, J. (2004):Matematikundervisning ll - udviklingsdyskalkuli.Fjerritslev:Landsforeningen af Læsepædagoger.Myklebust, H.R. & D. Johnson (1962): “Dyslexia in Children”.Exception-al Children,29(1), s. 14-25.Newmarch, B. (2005):Developing Numeracy, Supporting Achievement.Liecester: National Institute of Adult Continuing Education.Nordenbo, S.E., P. Allerup, H.L. Andersen, J. Dolin, H. Korp, M.S. Lar-sen, R. V. Olsen, S. Østergaard, M.M. Svendsen, N. Tiftikci &

R.E. Wendt (2009): ”Om pædagogisk brug af test”.Pædagogiskpsykologisk tidsskrift,46 (6).Nordic Research Network on Special Needs Education in Mathematics(2010):The Fifth Nordic Research Network on Special Needs Educationin Mathematics Conference proceedings.Nordic Research Network on Special Needs Education in Mathematics(2009):The Fourth Nordic Research Network on Special Needs Educa-tion in Mathematics Conference proceedings.Nordic Research Network on Special Needs Education in Mathematics(2007):The third Nordic Research Network on Special Needs Educationin Mathematics Conference proceedings.Nordic Research Network on Special Needs Education in Mathematics(2004):The second Nordic Research Network on Special Needs Educa-tion in Mathematics Conference proceedings.Nordiske forskersenminar om matematikkvansker (2001):Rapport fra den1.nordiske forskerseminar om matematikkvansker. Kristiansand, 25--28.september 2001.Orton-Flynn, S. & C.C.J. Richards (2000): “The design and evaluation ofan interactive calculator for children”.Digital Creativity,11(4), s.205-217.Ostad, S.A. (2008):Strategier, strategiobservasjon og strategiopplæring.Trond-heim: Læreboka forlagOstad, S.A. (2006): "Dysmatematikk: Et mulifaktorelt fenomen med ka-rakteristiske kjennetegn".SKOLEPSYKOLOGI,5, s. 27-39.Ostad, S.A. (2004):Matematikklæring og matematikkvansker - En artikkelsam-ling.Oslo: Institutt for spesialpedagogikk, UiO.Pind, P. (2008): ”Matematik-dansk - et særligt sprog”."Sprog og matematik- matematikkens sprog".Temahæfte.,s. 13-19.Pollak, D. (2009):Neurodiversity in Higher Education. Positive Responses to Spe-cific Learning Differences.Chichester, UK, Wiley-Blackwell.Poustie, J. (2000):Mathematics Solutions. How to Identify, Assess and ManageSpecific Learning Difficulties in Mathematics Pt. A.Taunton: NextGeneration.Price, N. & S. Youe (2000): “The Problems of Diagnosis and Remedia-tion of Dyscalculia”.For the Learning of Mathematics,20(3), s. 23-28.

Ravn, K. (2011):Matematik-speciallærere danner forening.Tilgængelig på:http://www.folkeskolen.dk/66252/matematik-speciallaerere-danner-forening . Besøgt d. 13-5-2013.Reed, J. & J.W. Rogers (2008):Child Neuropsychology. Concepts, Theory andPractice.Wiley-Blackwell Publishing.Reid, G. (2011):Dyslexia. A Complete Guide for Parents and Those Who HelpThem.Chichester: Wiley.Reid, G. (2009):The Routledge Companion to Dyslexia.London; Routledge.Reigosa-Crespo, V., M. Valdés-Sosa, B. Butterworth, N. Estévez, M.Rodrígues, E. Santos, P. Torres, R. Suárez & A. Lage (2012):“Basic Numerical Capacities and Prevalence of DevelopmentalDyscalculia: The Havana Survey”.Developmental Psychology,48(1),s. 123-135.Reikerås, E. (2004):“Democracy and Participation. A Challenge for SpecialNeeds Education in Mathematics”.Paper præsenteret på konfer-encen Proceedings of the 2ndNordic Research Conference onSpecial Needs Education in Mathematics.Reikerås, E. (2006): “Performance in Solving Arithmetic Problems: AComparison of Children with Different Levels of Achievementin Mathematics and Reading”.European Journal of Special NeedsEducation,21(3), s. 233-250.Reikerås, E. (2012): “The Mathematical Competencies of Toddlers Ex-pressed in their Play and Daily Life Activities in NorwegianKindergartens”.International Journal of Early Childhood,44(1), s.91-114.Riccio, C.A., J.R. Sullivan & M.J. Cohen (2012):Neuropsychological Assess-ment and Intervention for Childhood and Adolescent Disorders [El-ektronisk resurs].Hoboken, N.J.: John Wiley.Rosselli, M., E. Matute, N. Pinto & A. Ardila (2006): “Memory Abilitiesin Children with Subtypes of Dyscalculia”.Developmental Neuro-psychology, 30(3), s. 801-818.Rygvold, A.L. & T. Ogden (2008):Innføring i spesialpedagogikk.Oslo: Gyl-dendal Akademisk.Sahlin, B. (1997):Matematiksvårigheter och svårigheter när det gäller koncentrat-ion i grundskolan : en översikt av svensk forskning 1990-1995.Stock-holm: Statens skolverk .Schilling, S. & T. Prochinig (1991):Problemer med matematik.Vejen:Åløkke.

Shalev, R.S., O. Manor, B. Kerem, M. Ayali, N. Badichi, Y. Friedlander& V. Gross-Tsur (2001): “Developmental dyscalculia is a famil-iar learning disability”.Journal of Learning Disabilities, 34(1),s. 59-65.Sherman, H.J., L.I. Richardsom & G.J. Yard (2008):Teaching Learners whoStruggle with Mathematics. Systematic Intervention and Remediation.Up-per Saddle River, New Jersey.: Pearson/Merrill.Sigmundsson, H., S.K. Anholt & J.B. Talcott (2010): “Are Poor Mathe-matics Skills Associated with Visual Deficits in Temporal Pro-cessing?”Neuroscience Letters,469(2), s. 248-250.Simmons, F.R. & C. Singleton, C. (2009): “The Mathematical Strenghtsand Weaknesses of Children with Dyslexia”.Journal of Research inSpecial Educational Needs, 9(3),s. 154-163.Simmons, F.R. & C. Singleton (2008): “Do Weak Phonological Repre-sentations Impact on Arithmetic Development? A Review ofResearch into Arithmetic and Dyslexia”.Dyslexia,14(2), s. 77-94Sjukhusbiblioteken i Värmland(2012): Dyslexi - Lästips från sjukhusbib-lioteket Tilgængelig på:http://www.liv.se/Global/H%C3%A4lsa,%20v%C3%A5rd%20och%20patientinformation/Service/Sjukhusbiblioteken/Litteraturlistor/Dyslexi_20120223.pdf. Besøgt d. 15-8-2013.Sjöberg, G. (2008): ”Alla dessa IG – kan dyskalkyli vara förklaringen?”.Namnaren,3, s. 13-18.Sjöberg, G. (2006):Om det inte är dyskalkyli - vad är det då? En multimetod-studie av eleven i matematikproblem ur ett longitudinellt perspektiv.Umeå:Matematik, teknik och naturvetenskap. Ph.d.-afhandling.Sjöberg, G. & M. Nyroos, M. (2009):“Different Learners – Different Math?”.Paper præsenteret på konferencen. Proceedings of the 4th Nor-dic Research Conference on Special Needs Education in Math-ematicsSocialstyrelsen (2012):Vidensdeklaration. Socialstyrelsens vidensdeklaraion afsociale indsatser og metoder.Odense: Socialstyrelsen.Stanek, H. (2009):Ny forskning skal afdække talblindhed13-5-2013.Sterner, G. (2012):UR Samtiden - Matematik i kubik. En lärare + en elev =Intensivmatte.Sveriges Utbildningsradio.Sterner, G. & L. Lundberg (2002):Läs- och skrivsvårigheter och lärande i ma-tematik.Göteborg: Nationellt centrum för matematikutbildning,Göteborgs universitet.

Strandell, A. (2010):Dyslexi och dyskalkyli.Stockholm: Gothia.Street, B.V., D. Baker & A. Tomlin (2005):Navigating numeracies:home/school numeracy practices.Dordrecht: Springer.Swanson, H.L. & O. Jerman (2006): “Math Disabilities: A Selective Me-ta-Analysis of the literature”.Review of Educational Research,76(2),s. 249.Taipale, A. (2009):Matematiikan, lukemisen ja kirjoittamisen vaikeuksienpäällekkäistyminen nuoruusiässä.Joensuu: Joensuu UniversitetTemple, C.M. (1994): “The Cognitive Neuropsychology of the Devel-opmental Dyscalculias”.Cahiers de Psychologie Cognitive/Current Psy-chology of Cognition,13(3), s. 351-370.Temple, C.M. (1991): “Procedural Dyscalculia and Number Fact Dyscal-culia: Double Dissociation in Developmental Dyscalculia”.Cog-nitive Neuropsychology,8(2), s. 155-176.Temple, C.M. (1989): “Digit Dyslexia: A Category-specific Disorder inDevelopment Dyscalculia”.Cognitive Neuropsychology,6(1), s. 93-116.Undervisningsministeriet (2001).Klare Mål – matematik – Faghæfte 12.Til-gængelig på: http://pub.uvm.dk/2001/matematik/8.htm. Be-søgt d. 10-10-2013Undervisningsministeriet (2013). Tilgængelig på:http://uvm.dk/Uddannelser/Folkeskolen/De-nationale-test-og-evaluering/Internationale-evalueringer/PISA/PISA-2009?smarturl404=true. Besøgt d. 28-9-2013.UR (2010):UR Samtiden Tema: Räkna med framgång.Sveriges Utbildnings-radio.UR (2013):Skolministeriet. Det blev som jag befarade.Sveriges Utbildningsra-dio.UR (2012):Skoleministeriet: Dyskalkyli.Sveriges Utbildningsradio.Utoft, L. (2013): Planlæg dit fremskrift – erstat skam med stolthed. Til-gængelig på: http://www.ordblind.com/fremskridt.html. Besøgtd. 3-9-2012Valsa, K. & J. Murray, J. (2002):Unlocking Numeracy. A Guide for PrimarySchools.London: David Fulton.Vicario, C.M. (2012): “Temporal Abnormalities in Children with Devel-opmental Dyscalculia”.Developmental Neuropsychology,37(7), s.636-652.

SFI-RAPPORTER SIDEN 2012SFI-rapporter kan købes eller downloades gratis fra www.sfi.dk. Enkelterapporter er kun udkommet som netpublikationer, hvilket vil fremgå aflisten nedenfor.12:01Lyk-Jensen, S.V., A. Glad, J. Heidemann & M. Damgaard:Soldater efter udsendelse. En spørgeskemaundersøgelse.117 sider. e-ISBN: 978-87-7119-075-5. Netpublikation.Lausten, M., H. Hansen, A.-K. Mølholt, K.S. Vammen & A.-C.Legendre:Forebyggende foranstaltninger 14-17 år. Dialoggruppe – om fo-rebyggelse som alternativ til anbringelse. Delrapport 5.235 sider. ISBN:978-87-7119-078-6. e-ISBN: 978-87-7119- 079-3. Vejledendepris: 230,00 kr.Rostgaard, T., T.N. Brunner & T. Fridberg:Omsorg og livskvalitet iplejeboligen.150 sider. ISBN: 978-87-7119-080-9. e-ISBN: 978-87-7119-081-6. Vejledende pris: 150,00 kr.Mølholt, A.-K., S. Stage, J.H. Pejtersen & P. Thomsen:Efterværnfor tidligere anbragte unge. En videns- og erfaringsopsamling.222 sider.ISBN: 978-87-7119-082-3. e-ISBN: 978-87-7119-083-0. Vejle-dende pris: 220,00 kr.Ellerbæk, L.S. & A. Høst:Udlejningsredskaber i almene boliger. Enanalyse af brugen og effekterne af udlejningsredskaber i almene boligområder.

258 sider. ISBN: 978-87-7119-084-7. e-ISBN: 978-87-7119- 085-4. Vejledende pris: 250,00 kr.Høgelund, J.:Effekter af den beskæftigelsesrettede indsats for sygemeldte.En litteraturoversigt.112 sider. e-ISBN: 978-87-7119-086-1. Net-publikation.Rasmussen, P.S. & P.S. Olsen:Positiv adfærd i læring og samspil(PALS). En evaluering af en skoleomfattende intervention på 11 pilotsko-ler.159 sider. ISBN: 978-87-7119-087-8. e-ISBN: 978-87-7119-088-5. Vejledende pris: 150,00 kr.Fridberg, T. & M. Damgaard:Frivillige i hjemmeværnet 2011.120sider. ISBN: 978-87-7119-089-2. e-ISBN: 978-87-7119-090-8.Vejledende pris: 120,00 kr.Lyk-Jensen, S.V., J. Heidemann & A. Glad:Soldater – før og efterudsendelse. En analyse af motivation, økonomiske forhold og kriminalitet.164 sider. e-ISBN: 978-87-7119-091-5. Netpublikation.Bengtsson, S.:Vækstfaktorer på det specialiserede socialområde.120sider. ISBN: 978-87-7119-092-2. e-ISBN: 978-87-7119-093-9.Vejledende pris: 120,00 kr.Dines, A., V. Jakobsen, V.M. Jensen, S.S. Nielsen, S., K.C.Z.Pedersen, D.S. Petersen & K.M. Thorsen:Indsatser for tosprogedeelever. Kortlægning og analyse.162 sider. e-ISBN: 978-87-7119-094-6.Netpublikation.Christensen, E.:Nakuusa – vi vil og vi kan. En opfølgning på YouthForum i Ilulissat 2011.48 sider. e-ISBN: 978-87-7119-096-0. Net-publikation.Christensen, E.:Nakuusa – piumavugut saperatalu. 2011-mi ilulissaniYouth Forum pillugu nangitsineq.50 sider. e-ISBN: 978-87-7119-097-7. Netpublikation.Larsen, M. & L.S. Ellerbæk:Evaluering af jobplanen. Nuværende ogkommende pensionisters kendskab til og betydning af reglerne for at arbejde.111 sider. ISBN: 978-87-7119-100-4. e-ISBN: 978-87-7119-101-1. Vejledende pris: 110,00 kr.Larsen, M., H.B. Bach & A. Liversage:Pensionisters og efterlønsmod-tageres arbejdskraftpotentiale. Fokus på genindtræden.181 sider. ISBN:978-87-7119-102-8. e-ISBN: 978-87-7119-103-5. Vejledende pris:180,00 kr.Ottosen, M.H. & S. Stage:Delebørn i tal. En analyse af skilsmisse-børns samvær baseret på SFI’s børneforløbsundersøgelse.111 sider. ISBN:

978-87-7119-104-2. e-ISBN: 978-87-7119-105-9. Vejledende pris:110,00 kr.Nilsson, K. & H. Holt:En vurdering af arbejdsskadestyrelsens fastholdelse-scenter. Kommuners, fagforeningers, arbejdsgiveres og forsikringsselskaberserfaringer med fastholdelsescentret.89 sider. ISBN: 978-87-7119-106-6. e-ISBN: 978-87-7119- 107-3. Vejledende pris: 80,00 kr.Holt, H:Lokal løn på kommunale arbejdspladser. Forskelle i kvinders ogmænds løn.82 sider. e-ISBN: 978-87-7119-108-0. Netpublikation.Bengtsson, S. & M. Røgeskov:Et liv i egen bolig. Analyse af bostøtte tilborgere med sindslidelser.145 sider. ISBN: 978-87-7119-109-7. e-ISBN: 978-87-7119-110-3. Vejledende pris: 140,00 kr.Graversen, B:Effekter af virksomhedsrettet aktivering for udsatte ledige.En litteraturoversigt.72 sider. e-ISBN: 978-87-7119-112-7. Net-publikation.Albæk, K., H.B. Bach & S. Jensen:Effekter af mentorstøtte for udsatteledige. En litteraturoversigt.68 sider. e-ISBN: 978-87-7119-114-1.Netpublikation.Jensen, T.G., K. Weibel, M.K. Tørslev, L.L. Knudsen & S.J. Ja-cobsen:Måling af diskrimination på baggrund af etnisk oprindelse.134sider. ISBN: 978-87-7119-115-8, e-ISBN: 978-87-7119-116-5.Vejledende pris: 130,00 kr.Madsen, M.B. & K. Weibel:Delt viden. Aktiveringsindsatsen for ikke-arbejdsmarkedsparate kontanthjælpsmodtagere.152 sider. ISBN: 978-87-7119-117-2. e-ISBN: 978-87-7119-118-9. Vejledende pris:150,00 kr.Lyk-Jensen, S.V., J. Heidemann, A. Glad & C.D. Weatherall:Danske hjemvendte soldater. Soldaternes psykiske sundhedsprofil før og ef-ter udsendelse.210 sider. e-ISBN: 978-87-7119- 119-6. Netpublika-tion.Lausten, M., H. Hansen, K.S. Vammen & K. Vasegaard:Forebyg-gende foranstaltninger 18-22 år. Dialoggruppe – Om forebyggelse som al-ternativ til anbringelse. Delrapport 6.164 sider. ISBN: 978-87-7119-121-9. e-ISBN: 978-87-7119-122-6. Vejledende pris: 160,00 kr.Lauritzen, H.H., R.N. Brünner, P. Thomsen & M. Wüst:Ældresressourcer og behov. Status og udvikling på baggrund af Ældredatabasen.180 sider. ISBN: 978-87-7119-123-3. e-ISBN: 978-87-7119-124-0. Vejledende pris: 180,00 kr.

Høst, A.K, T. Fridberg, D.L. Stigaard & B. Boje-Kovacs:Nårfogeden banker på. Fogedsager og effektive udsættelser af lejere.422 sider.ISBN: 978-87-7119-125-7. e-ISBN: 978-87-7119-126-4. Vej-ledende pris 420,00 kr.Nielsen, H., A. Mølgaard & L. Dybdal:Procesevaluering af boligsocia-le indsatser. Delrapport 2. Kvalitativ kortlægning af Landsbyggefondens2006-2010-pulje med fokus på projektorganisering og samarbejde.118sider. e-ISBN: 978-87-7119-127-1. Netpublikation.Andrade, S.B.:Levekår i dansk landbrug. Analyse af sammenhængemellem risikofaktorer og dyrværnssager i landbruget fra 2000 til 2008.176 sider. ISBN: 978-87-7119-128-8. e-ISBN: 978-87-7119-129-5. Vejledende pris: 170,00 kr.Ottosen, M.H. (red.):15-åriges hverdagsliv og udfordringer. Rapport frafemte dataindsamling af forløbsundersøgelsen af børn født i 1995.348 si-der. ISBN: 978-87-7119-130-1. e-ISBN: 978-87-7119-131-8. Vej-ledende pris: 340,00 kr.Bach, H.B.:Arbejdsmarkedsparathed og selvforsørgelse.36 sider. e-ISBN: 978-87-7119-133-2. Netpublikation.Christensen, E. & A.P. Langhede:Evaluering af psykologhjælp tilbørn på krisecentre.61 sider. ISBN: 978-87-7811-197-5. Netpubli-kation. Udgivet af Ankestyrelsen og SFI.Termansen, T. & C.S. Sonne-Schmidt:Forebyggende fysisk træningtil ældre. En undersøgelse af effekten af en kort træningsindsats på ældresfysiske funktionsevne.64 sider. ISBN: 978-87-7119-135-6. e-ISBN:978-87-7119-136-3. Vejledende pris: 60,00 kr.Hansen, H., P.R. Skov & K.M. Sørensen:Støtte til udsatte børnefa-milier. En effektmåling af familiebehandling og praktisk pædagogiske støtte.112 sider. e-ISBN: 978-87-7119- 137-0. NetpublikationEllerbæk, L.S., V. Jakobsen, S. Jensen & H. Holt:Virksomhederssociale engagement. Årbog 2012.182 sider. ISBN: 978-87-7119-138-7. e-ISBN: 978-87-7119-139-4. Vejledende pris: 180,00 kr.Jakobsen, T.B., S.V. Lyk-Jensen & D.L. Stigaard:Lige muligheder –metodisk grundlag for en effektevaluering. Evalueringsrapport 2.82 sider.e-ISBN: 978-87-7487-140-0. Netpublikation.Kjeldsen, M.M., H.S. Houlberg & J. Høgelund:Handicap og be-skæftigelse. Udviklingen mellem 2002 og 2012.176 sider. ISBN: 978-87-7119-141-7. e-ISBN: 978-87-7119-142-4. Vejledende pris:170,00 kr.

Liversage, A, R. Bille & V. Jakobsen:Den danske au pair-ordning.281 sider. ISBN: ISBN 978-87-7119-143-1. e-ISBN: 978-87-7119-144-8. Vejledende pris 280,00 kr.Oldrup, H., A.K. Høst, A.A. Nielsen & B. Boje-Kovacs:Nårbørnefamilier sættes ud af deres lejebolig.222 sider. ISBN: 978-87-7119-145-5. e-ISBN: 978-87-7119-146-2. Vejledende pris: 220,00kr.Lausten, M., H. Hansen & V. M. Jensen:God praksis i forebyggendearbejde – samlet evaulering af dialogprojektet. Dialoggruppe – om forebyggelsesom alternativ til anbringelse.173 sider. ISBN: 978-87-7119-147-9. e-ISBN: 978-87-7119-148-6. Vejledende pris: 170,00 kr.Christensen, E.:Ilasiaq. Evaluering af en bo-enhed for udsatte børn.75sider. ISBN: 978-87-7119-149-3. e-ISBN: 978-87-7119-150-9.Vejledende pris: 70,00 kr.Christensen,E.:Ilasiaq.Meeqqanutaarlerinartorsiortunutnajugaqatigiiffimmik nalilersuineq.88 sider. ISBN: 978-87-7119-151-6.e-ISBN: 978-87-7119-152-3. Vejledende pris: 70,00 kr.Lausten, M., D. Andersen, P.R. Skov & A.A. Nielsen:Anbragte 15-åriges hverdagsliv og udfordringer. Rapport fra tredje dataindsamling afforløbsundersøgeslen af anbragte børn født i 1995.153 sider. ISBN: 978-87-7119-153-0. e-ISBN: 978-87-7119-154-7. Vejledende pris: 150,00 kr.Luckow, S.T. & V.L. Nielsen:Evaluering af ressource- og risikoskema.Tidlig identifikation af kriminalitetstruede børn og unge.90 sider. e-ISBN:978-87-7119-156-1. Netpublikation.Winter, S.C. & V.L. Nielsen (red.):Lærere, undervisning ogelevpræstationer i folkeskolen.265 sider. e-ISBN: 978-87-7119-158-5.Netpublikation.Kjeldsen, M.M., & J. Høgelund:Handicap og beskæftigelse i 2012.Regionale forskelle.59 sider. ISBN: 978-87-7119-159-2. e-ISBN: 978-87-7119-160-8. Vejledende pris: 60,00 kr.Manuel, C. & A. K. Jørgensen:Systematic review of youth crime preventionintervention – published 2008-2012.309 sider. e-ISBN: 978-87-7119-161-5. Netpublikation.Nilsson, K. & H. Holt:Halvering af dagpengeperioden og akutpakken.Erfaringer i jobcentre og A-kasser.80 sider. e-ISBN: 978-87-7119-162-2.Netpublikation.

Nielsen, A.A. & V.L. Nielsen:Evaluering af projekt SAMSPIL. Enudvidet mødregruppe til unge udsatte mødre.66 sider. e-ISBN: 978-87-7119-163-9. Netpublikation.Graversen, B.K., M. Larsen & J.N. Arendt:Kommunernes rammevilkårfor beskæftigelsesindsatsen.146 sider. e-ISBN: 978-87-7119- 168-4.NetpublikationBengtsson, S. & S. Ø. Gregersen:Integrerede indsatser over for menneskermed psykiske lidelser. En forskningsoversigt.106 sider. ISBN: 978-87-7119-169-1. e-ISBN: 978-87-7119-170-7. Vejledende pris: 100,00 kr.Christensen, E.:Ung i det grønlandske samfund. Unges holdning til og videnom sociale problemer og muligheder.58 sider. e-ISBN: 978-87-7119-171-4.Netpublikation.Christensen,E.:Kalaallitinuiaqatigiiviniinuusuttuaqqat.Inuusuttuaqqat inoqatigiinnermi ajornartorsiutit periarfissallu pillugitilisimasaat isummertariaasaallu.66 sider. e-ISBN: 978-87-7117-172-1. Netpublikation.Vammen, K.S. & M.N. Christoffersen:Unges selvskade ogspiseforstyrrelser. Kan social støtte gøre en forskel?156 sider. ISBN: 978-87-7119-173-8. e-ISBN: 978-87-7119-174-5. Vejledende pris: 150,00 kr.Fridberg, T. & M. Damgaard:Volunteers in the Danish Home Guard2011.120 sider. ISBN: 978-87-7119-175-2. e-ISBN: 978-87-7119-176-9.Luckow, S.T., T.B. Jakobsen, A.P. Langhede & J.Hyld Pejtersen:Bedre overgange for udsatte unge. Midtvejsevaluering af efterværnsinitiativet'Vejen til uddannelse og beskæftigelse'.98 sider. ISBN: 978-87-7119-177-6. e-ISBN: 978-87-7119-178-3. Vejledende pris: 90,00 kr.Benjaminsen, L. & H.H. Lauritzen:Hjemløshed i Danmark 2013.National kortlægning.182 sider. ISBN: 978-87-7119-179-0. e-ISBN:978-87-7119-180-6. Vejledende pris: 180,00 kr.Jacobsen, S. J., A. H. Klynge & H. Holt:Øremærkning af barsel til fædre.Et litteraturstudie.82 sider. ISBN: 978-87-7119-181-3. e-ISBN: 978-87-7119-182-0. Vejledende pris: 80,00 kr.Thuesen, F., H. B. Bach, K. Albæk, S. Jensen, N. L. Hansen & K.Weibel:Socialøkonomiske virksomheder i Danmark. Når udsatte bliveransatte.216 sider. ISBN: 978-87-7119-183-7. e-ISBN: 978-87-7119-184-4. Vejledende pris: 210,00 kr.

Larsen, Mona & H. S. B. Houlberg: Lønforskelle mellem mændog kvinder 2007-2011. 176 sider. ISBN: 978-87-7119-185-1. e-ISBN: 978-87-7119- 186-8. Vejledende pris: 170,00 kr.Larsen, M. & H.S.B. Houlberg:Mere uddannelse, mere i løn?50 si-der. e-ISBN: 978-87-7117-188-2. Netpublikation.Damgaard, M., Steffensen, T. & S. Bengtson:Hverdagsliv og leve-vilkår for mennesker med funktionsnedsættelse. En analyse af sammenhæn-ge mellem hverdagsliv, samliv, udsathed og type og grad af funktionsnedsæt-telse.193 sider. ISBN: 978-87-7119-189-9. e-ISBN: 978-87-7119-190-5. Vejledende pris: 190,00 kr.Holt, H. & K. Nilsson:Arbejdsfastholdelse af skadelidte medarbejdere.Virksomhedernes rolle og erfaringer.100 sider. ISBN: 978-87-7119-191-2. e-ISBN: 978-87-7119-192-9. Vejledende pris: 100,00 kr.Rosdahl, A., T. Fridberg, V. Jakobsen & M. Jørgensen:Færdighe-der i læsning, regning og problemløsning med IT i Danmark.410 sider.ISBN: 978-87-7119-193-6. e-ISBN: 978-87-7119-194-3. Vejle-dende pris: 400,00 kr.Rosdahl, A., T. Fridberg, V. Jakobsen & M. Jørgensen:Færdighe-der i læsning, regning og problemløsning med IT i Danmark. Sammenfat-ning af resultater fra PIAAC.62 sider. ISBN: 978-87-7119-195-0.e-ISBN: 978-87-7119-196-7. Vejledende pris: 60,00 kr.Christensen, E.:Børn i Mælkebøtten. Fra socialt udsat til mønsterbryder?125 sider. ISBN: 978-87-7119-197-4. e-ISBN: 978-87-7119- 198.Vejledende pris: 120,00 kr.Christensen, E.:Meeqqat Mælkebøttenimiittut. Isumaginninnikkutaarlerinartorsiortumiit ileqqunik allanngortitsisumut?149 sider. ISBN:978-87-7119-199-8. e-ISBN: 978-87-7119- 200-1. Vejledendepris: 140,00 kr.Bengtsson, S., H. E. D. Jørgensen & S. T. Grønfeldt:Sociale til-bud til mennesker med sindslidelse. Den første kortlægning på personniveau.130 sider. ISBN: 978-87-7119-201-8. e-ISBN: 978-87-7119- 202-5. Vejledende pris: 130,00 kr.Larsen, L. B. & S. Bengtson:Talblindhed. En forskningsoversigt.175sider. ISBN: 978-87-7119-205-6. e-ISBN: 978-87-7119- 206-3.Vejledende pris: 170,00 kr.Larsen, M.:Lønforskelle mellem mænd og kvinder i industrien. Medar-bejdere med håndværkspræget arbejde eller operatør- og monteringsarbej-de.978-87-7119-207-0.Netpublikation.

taLBLINDheDen ForSKnIngSoVerSIgtDenne rapport giver en oversigt over viden om talblindhed (også kaldet dyskalkuli) i Danmark, norge, Sverigeog Storbritannien. Mennesker med talblindhed mangler den grundlæggende evne til at forstå tal og mæng-der, hvilket kan være et stort handicap i hverdagen.rapporten beskriver den omfattende faglige diskussion, der har været om talblindhed i disse lande. På denbaggrund konkluderer forskerne, at det giver god mening at tale om talblindhed som en diagnose på linjemed ordblindhed. Forskerne opstiller også en samlet definition på talblindhed.rapporten beskriver desuden en række tests, indsatser og støtteformer for talblinde.Undersøgelsen er bestilt og finansieret af Undervisningsministeriet. rapporten indgår som et led i en størreproces for at målrette undervisningen i matematik.